Estimation
POLI_SCI 403: Probability and Statistics
Agenda
Random variables and random sampling
Estimation
Lab
Moving toward working with data
Mean squared error around \(\color{purple}c\)
\[ MSE = E[(X-\color{purple}c)^2] \]
We said that \(\color{purple} c =E[X]\) is the best predictor of \(X\) because it would minimize MSE
But \(E[X]\) is a theoretical quantity!
We can use data to approximate it
But how do we now if it is a good approximation?
Ingredients for statistical inference
Estimand \(\theta\)
Estimator \(\widehat \theta\)
Ingredients for statistical inference
Estimand \(\mu\)
Estimator \(\widehat \mu\)
Ingredients for statistical inference
Estimand \(\mu\)
Estimator \(\widehat \mu\)
Data \(X\)
Ingredients for statistical inference
Estimand \(\mu\)
Estimator \(\widehat \mu\)
Data \(X\)
Estimate \(\overline X\)
Ingredients for statistical inference
Estimand \(\mu\)
Estimator \(\widehat \mu\)
Data \(X\)
Estimate \(\overline X\)
Quantify uncertainty (next week)
\(X \rightarrow \overline{X} \rightarrow \widehat{\mu} \xrightarrow{\text{hopefully!}} \mu\)
Plug-in principle
Idea: Use sample quantities to approximate population parameters
We can replace \(\theta = T(F)\) with \(\widehat \theta = T(\widehat{F})\)
Where \(T(*)\) is a statistical functional
(Meaning whatever summary quantity of the CDF you care about)
Example
If we have
\[ T_E(F) = E[X] = \int_{-\infty}^{\infty} xdF(x) \]
We can plug-in
\[ T_E(\widehat F) = \widehat E[X] = \frac{1}{n} \sum_{i=1}^n x_i \]
Example
If we have
\[ T_E(F) = E[X] = \int_{-\infty}^{\infty} xdF(x) \]
We can plug-in
\[ T_E(\widehat F) = \widehat E[X] = \overline X \]
But how can we tell if any of this is legit?
Random sampling
Independent, identically distributed
We have random variables \(X_1, X_2, \ldots, X_n\)
with their respective CDFs \(F_1, F_2, \ldots, F_n\)
A collection of random variables is i.i.d. if they are:
Mutually independent
Identically distributed
Meaning we are taking \(n\) draws of the same (identical) random variable independently from each other?
Illustration
Question from the 2022 General Social Survey
In 2020, you remember that Joe Biden ran for President on the Democratic ticket against Donald Trump for the Republicans. Do you remember for sure whether or not you voted in that election?
- Yes, I voted
- No, I did not vote
- I was not eligible to vote
GSS Data
vote20 vote
1 1 1
2 1 1
3 1 1
4 1 1
5 1 1
6 1 1
7 2 0
8 1 1
9 1 1
10 1 1
11 1 1
12 1 1
13 1 1
14 1 1
15 1 1
16 1 1
17 1 1
18 1 1
19 2 0
20 1 1
21 3 0
22 1 1
23 1 1
24 1 1
25 1 1
26 1 1
27 1 1
28 1 1
29 1 1
30 1 1
31 1 1
32 1 1
33 1 1
34 1 1
35 2 0
36 1 1
37 1 1
38 1 1
39 1 1
40 2 0
41 1 1
42 3 0
43 1 1
44 2 0
45 1 1
46 1 1
47 1 1
48 1 1
49 2 0
50 1 1
51 1 1
52 3 0
53 2 0
54 1 1
55 1 1
56 2 0
57 1 1
58 2 0
59 1 1
60 2 0
61 1 1
62 1 1
63 2 0
64 1 1
65 1 1
66 2 0
67 2 0
68 1 1
69 1 1
70 1 1
71 1 1
72 1 1
73 1 1
74 1 1
75 1 1
76 1 1
77 1 1
78 1 1
79 2 0
80 1 1
81 1 1
82 1 1
83 1 1
84 1 1
85 1 1
86 1 1
87 1 1
88 1 1
89 1 1
90 1 1
91 1 1
92 1 1
93 1 1
94 2 0
95 1 1
96 2 0
97 1 1
98 1 1
99 1 1
100 1 1
101 1 1
102 1 1
103 1 1
104 1 1
105 1 1
106 1 1
107 2 0
108 1 1
109 1 1
110 2 0
111 3 0
112 2 0
113 2 0
114 2 0
115 2 0
116 1 1
117 1 1
118 1 1
119 1 1
120 3 0
121 1 1
122 1 1
123 1 1
124 1 1
125 2 0
126 3 0
127 1 1
128 1 1
129 2 0
130 2 0
131 1 1
132 1 1
133 1 1
134 1 1
135 1 1
136 1 1
137 1 1
138 1 1
139 1 1
140 1 1
141 1 1
142 2 0
143 1 1
144 3 0
145 1 1
146 2 0
147 1 1
148 1 1
149 1 1
150 1 1
151 2 0
152 1 1
153 1 1
154 2 0
155 1 1
156 1 1
157 1 1
158 1 1
159 1 1
160 2 0
161 1 1
162 1 1
163 1 1
164 1 1
165 1 1
166 2 0
167 2 0
168 1 1
169 1 1
170 1 1
171 1 1
172 1 1
173 2 0
174 1 1
175 1 1
176 1 1
177 1 1
178 2 0
179 1 1
180 1 1
181 1 1
182 1 1
183 1 1
184 1 1
185 1 1
186 1 1
187 1 1
188 1 1
189 2 0
190 1 1
191 1 1
192 1 1
193 1 1
194 1 1
195 1 1
196 2 0
197 1 1
198 3 0
199 1 1
200 2 0
201 1 1
202 1 1
203 1 1
204 1 1
205 3 0
206 1 1
207 2 0
208 1 1
209 1 1
210 1 1
211 1 1
212 1 1
213 1 1
214 1 1
215 1 1
216 1 1
217 1 1
218 1 1
219 1 1
220 1 1
221 1 1
222 1 1
223 1 1
224 1 1
225 1 1
226 2 0
227 1 1
228 1 1
229 1 1
230 1 1
231 1 1
232 2 0
233 1 1
234 3 0
235 3 0
236 2 0
237 1 1
238 1 1
239 1 1
240 1 1
241 2 0
242 1 1
243 1 1
244 1 1
245 1 1
246 2 0
247 1 1
248 2 0
249 1 1
250 1 1
251 3 0
252 1 1
253 1 1
254 3 0
255 1 1
256 1 1
257 1 1
258 1 1
259 1 1
260 1 1
261 3 0
262 1 1
263 1 1
264 1 1
265 2 0
266 2 0
267 1 1
268 2 0
269 1 1
270 1 1
271 1 1
272 1 1
273 1 1
274 2 0
275 1 1
276 1 1
277 1 1
278 1 1
279 1 1
280 1 1
281 2 0
282 1 1
283 1 1
284 1 1
285 1 1
286 1 1
287 1 1
288 1 1
289 3 0
290 1 1
291 1 1
292 1 1
293 1 1
294 1 1
295 2 0
296 1 1
297 3 0
298 1 1
299 1 1
300 1 1
301 1 1
302 1 1
303 1 1
304 1 1
305 2 0
306 2 0
307 2 0
308 1 1
309 2 0
310 1 1
311 1 1
312 2 0
313 1 1
314 2 0
315 3 0
316 1 1
317 2 0
318 1 1
319 1 1
320 1 1
321 1 1
322 1 1
323 1 1
324 1 1
325 1 1
326 1 1
327 1 1
328 2 0
329 1 1
330 1 1
331 1 1
332 2 0
333 1 1
334 1 1
335 1 1
336 2 0
337 2 0
338 1 1
339 1 1
340 1 1
341 1 1
342 1 1
343 1 1
344 1 1
345 1 1
346 1 1
347 1 1
348 1 1
349 1 1
350 1 1
351 2 0
352 2 0
353 1 1
354 1 1
355 1 1
356 3 0
357 1 1
358 1 1
359 1 1
360 1 1
361 1 1
362 1 1
363 1 1
364 1 1
365 1 1
366 1 1
367 2 0
368 1 1
369 1 1
370 1 1
371 1 1
372 2 0
373 1 1
374 1 1
375 1 1
376 1 1
377 3 0
378 1 1
379 1 1
380 2 0
381 2 0
382 2 0
383 2 0
384 1 1
385 2 0
386 1 1
387 1 1
388 1 1
389 1 1
390 1 1
391 1 1
392 1 1
393 2 0
394 1 1
395 1 1
396 1 1
397 1 1
398 2 0
399 1 1
400 1 1
401 1 1
402 1 1
403 1 1
404 1 1
405 1 1
406 1 1
407 2 0
408 1 1
409 1 1
410 1 1
411 1 1
412 2 0
413 2 0
414 1 1
415 1 1
416 1 1
417 1 1
418 2 0
419 1 1
420 1 1
421 1 1
422 1 1
423 1 1
424 1 1
425 2 0
426 1 1
427 1 1
428 1 1
429 3 0
430 1 1
431 1 1
432 1 1
433 1 1
434 1 1
435 1 1
436 3 0
437 2 0
438 1 1
439 1 1
440 1 1
441 2 0
442 2 0
443 1 1
444 1 1
445 1 1
446 1 1
447 1 1
448 1 1
449 2 0
450 1 1
451 1 1
452 1 1
453 1 1
454 1 1
455 3 0
456 1 1
457 2 0
458 1 1
459 1 1
460 1 1
461 1 1
462 1 1
463 1 1
464 1 1
465 1 1
466 2 0
467 2 0
468 3 0
469 2 0
470 2 0
471 1 1
472 1 1
473 1 1
474 2 0
475 2 0
476 1 1
477 1 1
478 1 1
479 1 1
480 1 1
481 1 1
482 1 1
483 1 1
484 1 1
485 1 1
486 1 1
487 1 1
488 2 0
489 1 1
490 3 0
491 1 1
492 2 0
493 1 1
494 1 1
495 3 0
496 1 1
497 1 1
498 1 1
499 1 1
500 1 1
501 1 1
502 2 0
503 1 1
504 1 1
505 1 1
506 1 1
507 1 1
508 1 1
509 1 1
510 1 1
511 3 0
512 3 0
513 1 1
514 1 1
515 2 0
516 1 1
517 1 1
518 3 0
519 1 1
520 1 1
521 1 1
522 1 1
523 2 0
524 1 1
525 2 0
526 1 1
527 1 1
528 1 1
529 1 1
530 1 1
531 1 1
532 1 1
533 1 1
534 1 1
535 1 1
536 3 0
537 1 1
538 1 1
539 1 1
540 3 0
541 1 1
542 1 1
543 1 1
544 1 1
545 1 1
546 1 1
547 1 1
548 1 1
549 1 1
550 1 1
551 1 1
552 1 1
553 1 1
554 1 1
555 3 0
556 1 1
557 1 1
558 1 1
559 1 1
560 1 1
561 1 1
562 1 1
563 1 1
564 1 1
565 1 1
566 2 0
567 2 0
568 1 1
569 1 1
570 2 0
571 1 1
572 3 0
573 1 1
574 1 1
575 1 1
576 1 1
577 1 1
578 2 0
579 1 1
580 1 1
581 1 1
582 1 1
583 1 1
584 1 1
585 1 1
586 1 1
587 1 1
588 1 1
589 1 1
590 2 0
591 1 1
592 2 0
593 1 1
594 2 0
595 1 1
596 2 0
597 1 1
598 1 1
599 2 0
600 1 1
601 1 1
602 1 1
603 1 1
604 1 1
605 1 1
606 1 1
607 1 1
608 1 1
609 1 1
610 1 1
611 1 1
612 1 1
613 1 1
614 1 1
615 1 1
616 2 0
617 1 1
618 1 1
619 1 1
620 1 1
621 1 1
622 1 1
623 3 0
624 1 1
625 1 1
626 1 1
627 1 1
628 1 1
629 1 1
630 1 1
631 1 1
632 1 1
633 1 1
634 2 0
635 1 1
636 1 1
637 1 1
638 1 1
639 2 0
640 1 1
641 1 1
642 1 1
643 1 1
644 2 0
645 2 0
646 1 1
647 3 0
648 1 1
649 1 1
650 1 1
651 1 1
652 2 0
653 3 0
654 1 1
655 1 1
656 1 1
657 1 1
658 3 0
659 1 1
660 1 1
661 1 1
662 1 1
663 1 1
664 1 1
665 1 1
666 1 1
667 1 1
668 1 1
669 1 1
670 1 1
671 1 1
672 1 1
673 1 1
674 3 0
675 1 1
676 1 1
677 1 1
678 1 1
679 1 1
680 1 1
681 1 1
682 1 1
683 1 1
684 1 1
685 1 1
686 1 1
687 1 1
688 2 0
689 1 1
690 1 1
691 1 1
692 2 0
693 1 1
694 1 1
695 1 1
696 1 1
697 2 0
698 1 1
699 1 1
700 1 1
701 1 1
702 2 0
703 1 1
704 1 1
705 1 1
706 1 1
707 1 1
708 1 1
709 1 1
710 1 1
711 1 1
712 1 1
713 1 1
714 1 1
715 1 1
716 1 1
717 1 1
718 2 0
719 3 0
720 1 1
721 2 0
722 1 1
723 2 0
724 1 1
725 1 1
726 1 1
727 1 1
728 1 1
729 1 1
730 1 1
731 1 1
732 1 1
733 1 1
734 1 1
735 1 1
736 1 1
737 1 1
738 1 1
739 1 1
740 1 1
741 1 1
742 1 1
743 1 1
744 2 0
745 1 1
746 2 0
747 1 1
748 1 1
749 1 1
750 1 1
751 1 1
752 1 1
753 2 0
754 1 1
755 1 1
756 1 1
757 1 1
758 1 1
759 3 0
760 2 0
761 1 1
762 1 1
763 1 1
764 1 1
765 2 0
766 1 1
767 1 1
768 1 1
769 1 1
770 1 1
771 3 0
772 1 1
773 1 1
774 1 1
775 2 0
776 1 1
777 2 0
778 1 1
779 2 0
780 1 1
781 1 1
782 1 1
783 2 0
784 1 1
785 1 1
786 1 1
787 2 0
788 1 1
789 1 1
790 2 0
791 1 1
792 1 1
793 1 1
794 1 1
795 1 1
796 2 0
797 1 1
798 1 1
799 1 1
800 1 1
801 1 1
802 1 1
803 1 1
804 1 1
805 2 0
806 1 1
807 1 1
808 1 1
809 2 0
810 1 1
811 1 1
812 1 1
813 3 0
814 1 1
815 1 1
816 3 0
817 1 1
818 1 1
819 1 1
820 1 1
821 1 1
822 1 1
823 1 1
824 1 1
825 1 1
826 3 0
827 1 1
828 1 1
829 1 1
830 3 0
831 3 0
832 1 1
833 1 1
834 1 1
835 1 1
836 1 1
837 1 1
838 1 1
839 1 1
840 1 1
841 1 1
842 1 1
843 1 1
844 1 1
845 1 1
846 1 1
847 1 1
848 1 1
849 1 1
850 1 1
851 1 1
852 3 0
853 1 1
854 1 1
855 1 1
856 1 1
857 1 1
858 1 1
859 1 1
860 1 1
861 1 1
862 1 1
863 1 1
864 2 0
865 1 1
866 1 1
867 2 0
868 1 1
869 2 0
870 1 1
871 1 1
872 2 0
873 1 1
874 1 1
875 1 1
876 1 1
877 1 1
878 2 0
879 2 0
880 3 0
881 2 0
882 1 1
883 3 0
884 1 1
885 1 1
886 2 0
887 3 0
888 2 0
889 2 0
890 3 0
891 3 0
892 3 0
893 1 1
894 3 0
895 3 0
896 2 0
897 2 0
898 1 1
899 2 0
900 3 0
901 1 1
902 1 1
903 1 1
904 1 1
905 2 0
906 2 0
907 1 1
908 2 0
909 1 1
910 1 1
911 2 0
912 2 0
913 1 1
914 1 1
915 1 1
916 2 0
917 1 1
918 1 1
919 1 1
920 2 0
921 1 1
922 1 1
923 2 0
924 1 1
925 3 0
926 1 1
927 2 0
928 2 0
929 2 0
930 1 1
931 2 0
932 1 1
933 1 1
934 1 1
935 1 1
936 2 0
937 1 1
938 1 1
939 1 1
940 1 1
941 1 1
942 1 1
943 1 1
944 1 1
945 1 1
946 1 1
947 1 1
948 1 1
949 1 1
950 1 1
951 1 1
952 1 1
953 1 1
954 2 0
955 1 1
956 1 1
957 1 1
958 1 1
959 1 1
960 1 1
961 1 1
962 1 1
963 1 1
964 1 1
965 1 1
966 2 0
967 1 1
968 1 1
969 1 1
970 1 1
971 3 0
972 2 0
973 3 0
974 1 1
975 1 1
976 1 1
977 2 0
978 3 0
979 2 0
980 1 1
981 1 1
982 1 1
983 1 1
984 2 0
985 1 1
986 1 1
987 1 1
988 2 0
989 1 1
990 2 0
991 1 1
992 2 0
993 2 0
994 1 1
995 1 1
996 1 1
997 1 1
998 1 1
999 1 1
1000 2 0
1001 1 1
1002 1 1
1003 1 1
1004 2 0
1005 1 1
1006 1 1
1007 1 1
1008 1 1
1009 1 1
1010 1 1
1011 1 1
1012 3 0
1013 1 1
1014 1 1
1015 2 0
1016 2 0
1017 2 0
1018 1 1
1019 1 1
1020 2 0
1021 2 0
1022 1 1
1023 2 0
1024 1 1
1025 1 1
1026 1 1
1027 3 0
1028 1 1
1029 1 1
1030 1 1
1031 1 1
1032 2 0
1033 1 1
1034 1 1
1035 1 1
1036 2 0
1037 1 1
1038 1 1
1039 1 1
1040 1 1
1041 1 1
1042 2 0
1043 1 1
1044 1 1
1045 1 1
1046 1 1
1047 1 1
1048 1 1
1049 2 0
1050 1 1
1051 2 0
1052 2 0
1053 2 0
1054 1 1
1055 1 1
1056 1 1
1057 2 0
1058 1 1
1059 1 1
1060 1 1
1061 1 1
1062 1 1
1063 1 1
1064 1 1
1065 1 1
1066 1 1
1067 1 1
1068 1 1
1069 1 1
1070 1 1
1071 1 1
1072 2 0
1073 1 1
1074 1 1
1075 1 1
1076 1 1
1077 3 0
1078 2 0
1079 1 1
1080 2 0
1081 2 0
1082 2 0
1083 1 1
1084 2 0
1085 1 1
1086 1 1
1087 1 1
1088 1 1
1089 2 0
1090 1 1
1091 3 0
1092 1 1
1093 1 1
1094 1 1
1095 1 1
1096 1 1
1097 2 0
1098 1 1
1099 1 1
1100 2 0
1101 1 1
1102 1 1
1103 1 1
1104 2 0
1105 2 0
1106 1 1
1107 2 0
1108 1 1
1109 2 0
1110 1 1
1111 1 1
1112 2 0
1113 1 1
1114 1 1
1115 2 0
1116 1 1
1117 3 0
1118 2 0
1119 2 0
1120 1 1
1121 2 0
1122 1 1
1123 2 0
1124 1 1
1125 1 1
1126 1 1
1127 2 0
1128 1 1
1129 2 0
1130 1 1
1131 1 1
1132 1 1
1133 2 0
1134 1 1
1135 1 1
1136 2 0
1137 1 1
1138 2 0
1139 1 1
1140 1 1
1141 1 1
1142 2 0
1143 1 1
1144 2 0
1145 2 0
1146 2 0
1147 1 1
1148 1 1
1149 1 1
1150 1 1
1151 1 1
1152 1 1
1153 3 0
1154 1 1
1155 1 1
1156 1 1
1157 1 1
1158 1 1
1159 1 1
1160 1 1
1161 1 1
1162 1 1
1163 2 0
1164 1 1
1165 2 0
1166 1 1
1167 1 1
1168 2 0
1169 1 1
1170 1 1
1171 1 1
1172 1 1
1173 2 0
1174 1 1
1175 1 1
1176 1 1
1177 1 1
1178 1 1
1179 2 0
1180 1 1
1181 1 1
1182 1 1
1183 2 0
1184 1 1
1185 1 1
1186 2 0
1187 2 0
1188 2 0
1189 1 1
1190 1 1
1191 2 0
1192 1 1
1193 1 1
1194 2 0
1195 2 0
1196 2 0
1197 2 0
1198 1 1
1199 3 0
1200 1 1
1201 1 1
1202 1 1
1203 1 1
1204 1 1
1205 1 1
1206 1 1
1207 1 1
1208 1 1
1209 2 0
1210 1 1
1211 2 0
1212 1 1
1213 2 0
1214 1 1
1215 1 1
1216 1 1
1217 1 1
1218 1 1
1219 2 0
1220 1 1
1221 1 1
1222 1 1
1223 2 0
1224 1 1
1225 2 0
1226 1 1
1227 1 1
1228 1 1
1229 2 0
1230 1 1
1231 2 0
1232 1 1
1233 1 1
1234 1 1
1235 1 1
1236 1 1
1237 1 1
1238 1 1
1239 1 1
1240 1 1
1241 1 1
1242 1 1
1243 1 1
1244 1 1
1245 1 1
1246 1 1
1247 1 1
1248 1 1
1249 1 1
1250 1 1
1251 1 1
1252 1 1
1253 2 0
1254 1 1
1255 1 1
1256 2 0
1257 1 1
1258 1 1
1259 1 1
1260 1 1
1261 1 1
1262 2 0
1263 1 1
1264 1 1
1265 1 1
1266 1 1
1267 1 1
1268 1 1
1269 2 0
1270 1 1
1271 1 1
1272 1 1
1273 2 0
1274 1 1
1275 1 1
1276 1 1
1277 2 0
1278 2 0
1279 1 1
1280 1 1
1281 3 0
1282 1 1
1283 2 0
1284 2 0
1285 1 1
1286 1 1
1287 1 1
1288 2 0
1289 1 1
1290 3 0
1291 1 1
1292 1 1
1293 1 1
1294 2 0
1295 1 1
1296 1 1
1297 3 0
1298 2 0
1299 1 1
1300 1 1
1301 1 1
1302 1 1
1303 2 0
1304 1 1
1305 1 1
1306 1 1
1307 1 1
1308 1 1
1309 1 1
1310 2 0
1311 1 1
1312 1 1
1313 2 0
1314 3 0
1315 1 1
1316 1 1
1317 1 1
1318 1 1
1319 2 0
1320 1 1
1321 1 1
1322 2 0
1323 2 0
1324 1 1
1325 1 1
1326 1 1
1327 1 1
1328 1 1
1329 1 1
1330 1 1
1331 2 0
1332 1 1
1333 1 1
1334 1 1
1335 2 0
1336 2 0
1337 1 1
1338 2 0
1339 1 1
1340 1 1
1341 1 1
1342 1 1
1343 2 0
1344 2 0
1345 1 1
1346 1 1
1347 1 1
1348 1 1
1349 2 0
1350 1 1
1351 1 1
1352 1 1
1353 1 1
1354 1 1
1355 2 0
1356 1 1
1357 2 0
1358 1 1
1359 2 0
1360 2 0
1361 1 1
1362 1 1
1363 1 1
1364 1 1
1365 1 1
1366 1 1
1367 1 1
1368 1 1
1369 1 1
1370 1 1
1371 3 0
1372 1 1
1373 2 0
1374 1 1
1375 1 1
1376 1 1
1377 1 1
1378 1 1
1379 1 1
1380 2 0
1381 1 1
1382 1 1
1383 1 1
1384 1 1
1385 1 1
1386 1 1
1387 1 1
1388 1 1
1389 1 1
1390 1 1
1391 1 1
1392 1 1
1393 1 1
1394 1 1
1395 1 1
1396 2 0
1397 1 1
1398 1 1
1399 1 1
1400 2 0
1401 1 1
1402 1 1
1403 1 1
1404 2 0
1405 1 1
1406 1 1
1407 1 1
1408 1 1
1409 1 1
1410 1 1
1411 1 1
1412 1 1
1413 1 1
1414 2 0
1415 1 1
1416 1 1
1417 1 1
1418 1 1
1419 1 1
1420 1 1
1421 1 1
1422 1 1
1423 1 1
1424 1 1
1425 2 0
1426 1 1
1427 2 0
1428 2 0
1429 1 1
1430 2 0
1431 2 0
1432 1 1
1433 1 1
1434 1 1
1435 1 1
1436 1 1
1437 1 1
1438 2 0
1439 2 0
1440 1 1
1441 1 1
1442 2 0
1443 1 1
1444 1 1
1445 1 1
1446 2 0
1447 2 0
1448 2 0
1449 1 1
1450 1 1
1451 3 0
1452 1 1
1453 1 1
1454 2 0
1455 1 1
1456 1 1
1457 2 0
1458 1 1
1459 2 0
1460 1 1
1461 2 0
1462 1 1
1463 1 1
1464 1 1
1465 1 1
1466 1 1
1467 1 1
1468 1 1
1469 1 1
1470 1 1
1471 1 1
1472 2 0
1473 1 1
1474 2 0
1475 1 1
1476 1 1
1477 1 1
1478 1 1
1479 1 1
1480 1 1
1481 1 1
1482 1 1
1483 1 1
1484 1 1
1485 1 1
1486 1 1
1487 1 1
1488 1 1
1489 1 1
1490 3 0
1491 1 1
1492 1 1
1493 2 0
1494 1 1
1495 2 0
1496 2 0
1497 1 1
1498 1 1
1499 2 0
1500 1 1
1501 1 1
1502 2 0
1503 1 1
1504 1 1
1505 1 1
1506 1 1
1507 1 1
1508 1 1
1509 1 1
1510 1 1
1511 3 0
1512 1 1
1513 1 1
1514 1 1
1515 1 1
1516 1 1
1517 1 1
1518 1 1
1519 1 1
1520 2 0
1521 1 1
1522 1 1
1523 1 1
1524 1 1
1525 1 1
1526 3 0
1527 2 0
1528 2 0
1529 1 1
1530 2 0
1531 2 0
1532 3 0
1533 2 0
1534 1 1
1535 1 1
1536 1 1
1537 1 1
1538 1 1
1539 1 1
1540 1 1
1541 1 1
1542 2 0
1543 1 1
1544 1 1
1545 1 1
1546 1 1
1547 1 1
1548 1 1
1549 1 1
1550 1 1
1551 1 1
1552 2 0
1553 1 1
1554 1 1
1555 2 0
1556 2 0
1557 3 0
1558 1 1
1559 1 1
1560 1 1
1561 1 1
1562 1 1
1563 3 0
1564 1 1
1565 1 1
1566 1 1
1567 1 1
1568 1 1
1569 1 1
1570 1 1
1571 1 1
1572 1 1
1573 1 1
1574 1 1
1575 2 0
1576 1 1
1577 1 1
1578 1 1
1579 1 1
1580 1 1
1581 1 1
1582 3 0
1583 2 0
1584 2 0
1585 2 0
1586 3 0
1587 2 0
1588 2 0
1589 3 0
1590 3 0
1591 1 1
1592 2 0
1593 2 0
1594 1 1
1595 1 1
1596 3 0
1597 1 1
1598 1 1
1599 1 1
1600 1 1
1601 3 0
1602 2 0
1603 1 1
1604 2 0
1605 1 1
1606 1 1
1607 2 0
1608 1 1
1609 1 1
1610 2 0
1611 1 1
1612 2 0
1613 1 1
1614 2 0
1615 1 1
1616 1 1
1617 1 1
1618 1 1
1619 1 1
1620 1 1
1621 3 0
1622 1 1
1623 3 0
1624 2 0
1625 2 0
1626 1 1
1627 2 0
1628 1 1
1629 1 1
1630 2 0
1631 2 0
1632 1 1
1633 2 0
1634 3 0
1635 1 1
1636 1 1
1637 2 0
1638 2 0
1639 1 1
1640 1 1
1641 2 0
1642 1 1
1643 1 1
1644 3 0
1645 1 1
1646 1 1
1647 2 0
1648 1 1
1649 1 1
1650 1 1
1651 1 1
1652 1 1
1653 1 1
1654 2 0
1655 1 1
1656 1 1
1657 1 1
1658 2 0
1659 1 1
1660 1 1
1661 1 1
1662 1 1
1663 1 1
1664 1 1
1665 2 0
1666 1 1
1667 1 1
1668 1 1
1669 1 1
1670 1 1
1671 2 0
1672 1 1
1673 1 1
1674 1 1
1675 2 0
1676 1 1
1677 2 0
1678 1 1
1679 1 1
1680 1 1
1681 1 1
1682 1 1
1683 1 1
1684 1 1
1685 1 1
1686 1 1
1687 3 0
1688 1 1
1689 2 0
1690 1 1
1691 1 1
1692 1 1
1693 2 0
1694 1 1
1695 1 1
1696 1 1
1697 1 1
1698 1 1
1699 1 1
1700 2 0
1701 2 0
1702 1 1
1703 1 1
1704 2 0
1705 1 1
1706 1 1
1707 2 0
1708 3 0
1709 1 1
1710 1 1
1711 3 0
1712 2 0
1713 1 1
1714 1 1
1715 1 1
1716 1 1
1717 1 1
1718 2 0
1719 1 1
1720 1 1
1721 1 1
1722 1 1
1723 1 1
1724 1 1
1725 1 1
1726 1 1
1727 1 1
1728 1 1
1729 1 1
1730 1 1
1731 2 0
1732 1 1
1733 1 1
1734 1 1
1735 1 1
1736 1 1
1737 2 0
1738 1 1
1739 3 0
1740 1 1
1741 2 0
1742 1 1
1743 1 1
1744 1 1
1745 1 1
1746 1 1
1747 1 1
1748 1 1
1749 1 1
1750 1 1
1751 1 1
1752 1 1
1753 1 1
1754 1 1
1755 1 1
1756 1 1
1757 1 1
1758 1 1
1759 1 1
1760 1 1
1761 1 1
1762 1 1
1763 1 1
1764 1 1
1765 3 0
1766 1 1
1767 1 1
1768 1 1
1769 1 1
1770 1 1
1771 1 1
1772 1 1
1773 1 1
1774 1 1
1775 1 1
1776 1 1
1777 1 1
1778 1 1
1779 1 1
1780 1 1
1781 1 1
1782 1 1
1783 3 0
1784 1 1
1785 1 1
1786 1 1
1787 1 1
1788 2 0
1789 1 1
1790 2 0
1791 2 0
1792 2 0
1793 2 0
1794 2 0
1795 2 0
1796 1 1
1797 1 1
1798 3 0
1799 2 0
1800 1 1
1801 1 1
1802 2 0
1803 2 0
1804 1 1
1805 2 0
1806 1 1
1807 1 1
1808 1 1
1809 1 1
1810 1 1
1811 1 1
1812 1 1
1813 1 1
1814 1 1
1815 3 0
1816 1 1
1817 1 1
1818 2 0
1819 2 0
1820 2 0
1821 1 1
1822 2 0
1823 1 1
1824 1 1
1825 2 0
1826 1 1
1827 2 0
1828 1 1
1829 1 1
1830 1 1
1831 1 1
1832 1 1
1833 2 0
1834 1 1
1835 1 1
1836 1 1
1837 1 1
1838 1 1
1839 1 1
1840 2 0
1841 1 1
1842 1 1
1843 1 1
1844 1 1
1845 1 1
1846 1 1
1847 1 1
1848 1 1
1849 1 1
1850 1 1
1851 1 1
1852 1 1
1853 2 0
1854 1 1
1855 2 0
1856 1 1
1857 1 1
1858 2 0
1859 2 0
1860 1 1
1861 1 1
1862 1 1
1863 1 1
1864 1 1
1865 2 0
1866 2 0
1867 1 1
1868 1 1
1869 1 1
1870 1 1
1871 1 1
1872 1 1
1873 1 1
1874 1 1
1875 1 1
1876 3 0
1877 1 1
1878 1 1
1879 1 1
1880 1 1
1881 1 1
1882 1 1
1883 1 1
1884 1 1
1885 1 1
1886 2 0
1887 1 1
1888 2 0
1889 2 0
1890 2 0
1891 1 1
1892 2 0
1893 2 0
1894 1 1
1895 1 1
1896 1 1
1897 1 1
1898 1 1
1899 3 0
1900 1 1
1901 1 1
1902 1 1
1903 1 1
1904 1 1
1905 1 1
1906 1 1
1907 1 1
1908 1 1
1909 1 1
1910 1 1
1911 1 1
1912 1 1
1913 1 1
1914 1 1
1915 2 0
1916 1 1
1917 2 0
1918 2 0
1919 1 1
1920 1 1
1921 1 1
1922 1 1
1923 1 1
1924 1 1
1925 1 1
1926 1 1
1927 1 1
1928 1 1
1929 1 1
1930 1 1
1931 2 0
1932 2 0
1933 1 1
1934 2 0
1935 1 1
1936 1 1
1937 2 0
1938 2 0
1939 1 1
1940 1 1
1941 1 1
1942 1 1
1943 1 1
1944 1 1
1945 1 1
1946 1 1
1947 1 1
1948 1 1
1949 1 1
1950 1 1
1951 1 1
1952 1 1
1953 1 1
1954 1 1
1955 2 0
1956 1 1
1957 2 0
1958 2 0
1959 1 1
1960 2 0
1961 1 1
1962 2 0
1963 1 1
1964 1 1
1965 1 1
1966 1 1
1967 2 0
1968 1 1
1969 1 1
1970 1 1
1971 1 1
1972 1 1
1973 2 0
1974 2 0
1975 1 1
1976 1 1
1977 3 0
1978 1 1
1979 1 1
1980 1 1
1981 1 1
1982 1 1
1983 1 1
1984 1 1
1985 2 0
1986 1 1
1987 1 1
1988 1 1
1989 1 1
1990 1 1
1991 1 1
1992 2 0
1993 1 1
1994 1 1
1995 1 1
1996 2 0
1997 1 1
1998 1 1
1999 1 1
2000 1 1
2001 1 1
2002 1 1
2003 1 1
2004 1 1
2005 1 1
2006 1 1
2007 1 1
2008 1 1
2009 1 1
2010 1 1
2011 1 1
2012 1 1
2013 3 0
2014 1 1
2015 1 1
2016 2 0
2017 1 1
2018 1 1
2019 2 0
2020 1 1
2021 1 1
2022 2 0
2023 1 1
2024 2 0
2025 1 1
2026 1 1
2027 2 0
2028 1 1
2029 1 1
2030 1 1
2031 1 1
2032 1 1
2033 1 1
2034 1 1
2035 1 1
2036 1 1
2037 2 0
2038 1 1
2039 3 0
2040 1 1
2041 1 1
2042 1 1
2043 1 1
2044 1 1
2045 3 0
2046 1 1
2047 1 1
2048 1 1
2049 1 1
2050 1 1
2051 1 1
2052 2 0
2053 2 0
2054 2 0
2055 2 0
2056 3 0
2057 1 1
2058 1 1
2059 1 1
2060 1 1
2061 1 1
2062 1 1
2063 1 1
2064 1 1
2065 1 1
2066 1 1
2067 1 1
2068 1 1
2069 2 0
2070 1 1
2071 2 0
2072 2 0
2073 1 1
2074 1 1
2075 1 1
2076 1 1
2077 2 0
2078 1 1
2079 3 0
2080 1 1
2081 1 1
2082 2 0
2083 1 1
2084 1 1
2085 1 1
2086 1 1
2087 1 1
2088 1 1
2089 1 1
2090 1 1
2091 1 1
2092 3 0
2093 1 1
2094 3 0
2095 2 0
2096 1 1
2097 1 1
2098 2 0
2099 1 1
2100 1 1
2101 2 0
2102 2 0
2103 2 0
2104 1 1
2105 1 1
2106 1 1
2107 1 1
2108 1 1
2109 1 1
2110 1 1
2111 1 1
2112 1 1
2113 1 1
2114 1 1
2115 1 1
2116 1 1
2117 1 1
2118 1 1
2119 1 1
2120 1 1
2121 2 0
2122 1 1
2123 2 0
2124 1 1
2125 1 1
2126 1 1
2127 1 1
2128 1 1
2129 1 1
2130 1 1
2131 1 1
2132 1 1
2133 1 1
2134 1 1
2135 1 1
2136 2 0
2137 1 1
2138 1 1
2139 1 1
2140 1 1
2141 2 0
2142 1 1
2143 1 1
2144 1 1
2145 2 0
2146 1 1
2147 1 1
2148 2 0
2149 1 1
2150 1 1
2151 2 0
2152 1 1
2153 1 1
2154 1 1
2155 1 1
2156 2 0
2157 2 0
2158 2 0
2159 1 1
2160 1 1
2161 1 1
2162 1 1
2163 1 1
2164 3 0
2165 1 1
2166 2 0
2167 1 1
2168 2 0
2169 2 0
2170 2 0
2171 2 0
2172 3 0
2173 1 1
2174 1 1
2175 1 1
2176 1 1
2177 1 1
2178 1 1
2179 1 1
2180 1 1
2181 1 1
2182 1 1
2183 1 1
2184 3 0
2185 2 0
2186 2 0
2187 1 1
2188 1 1
2189 2 0
2190 1 1
2191 3 0
2192 1 1
2193 2 0
2194 1 1
2195 1 1
2196 1 1
2197 1 1
2198 3 0
2199 1 1
2200 1 1
2201 1 1
2202 1 1
2203 1 1
2204 1 1
2205 1 1
2206 1 1
2207 1 1
2208 2 0
2209 2 0
2210 1 1
2211 1 1
2212 1 1
2213 1 1
2214 1 1
2215 1 1
2216 1 1
2217 1 1
2218 2 0
2219 1 1
2220 1 1
2221 2 0
2222 2 0
2223 2 0
2224 1 1
2225 1 1
2226 1 1
2227 1 1
2228 1 1
2229 1 1
2230 1 1
2231 1 1
2232 1 1
2233 1 1
2234 2 0
2235 2 0
2236 3 0
2237 1 1
2238 1 1
2239 1 1
2240 1 1
2241 1 1
2242 1 1
2243 1 1
2244 1 1
2245 1 1
2246 1 1
2247 3 0
2248 1 1
2249 3 0
2250 1 1
2251 1 1
2252 1 1
2253 1 1
2254 2 0
2255 1 1
2256 1 1
2257 1 1
2258 1 1
2259 1 1
2260 1 1
2261 1 1
2262 1 1
2263 1 1
2264 1 1
2265 1 1
2266 1 1
2267 1 1
2268 1 1
2269 2 0
2270 2 0
2271 1 1
2272 1 1
2273 1 1
2274 1 1
2275 1 1
2276 1 1
2277 1 1
2278 2 0
2279 1 1
2280 1 1
2281 1 1
2282 1 1
2283 1 1
2284 2 0
2285 1 1
2286 1 1
2287 2 0
2288 1 1
2289 1 1
2290 1 1
2291 1 1
2292 1 1
2293 3 0
2294 1 1
2295 1 1
2296 1 1
2297 1 1
2298 1 1
2299 1 1
2300 1 1
2301 1 1
2302 1 1
2303 2 0
2304 1 1
2305 1 1
2306 2 0
2307 1 1
2308 3 0
2309 2 0
2310 1 1
2311 1 1
2312 1 1
2313 1 1
2314 1 1
2315 1 1
2316 1 1
2317 1 1
2318 1 1
2319 1 1
2320 1 1
2321 1 1
2322 1 1
2323 1 1
2324 1 1
2325 3 0
2326 1 1
2327 2 0
2328 1 1
2329 1 1
2330 1 1
2331 3 0
2332 2 0
2333 1 1
2334 1 1
2335 2 0
2336 1 1
2337 1 1
2338 2 0
2339 2 0
2340 1 1
2341 2 0
2342 2 0
2343 1 1
2344 1 1
2345 1 1
2346 2 0
2347 2 0
2348 1 1
2349 1 1
2350 1 1
2351 1 1
2352 1 1
2353 1 1
2354 1 1
2355 3 0
2356 1 1
2357 2 0
2358 1 1
2359 1 1
2360 1 1
2361 1 1
2362 1 1
2363 1 1
2364 3 0
2365 1 1
2366 1 1
2367 2 0
2368 1 1
2369 2 0
2370 1 1
2371 1 1
2372 2 0
2373 3 0
2374 2 0
2375 2 0
2376 1 1
2377 1 1
2378 1 1
2379 1 1
2380 1 1
2381 1 1
2382 1 1
2383 2 0
2384 1 1
2385 1 1
2386 2 0
2387 1 1
2388 1 1
2389 1 1
2390 1 1
2391 1 1
2392 3 0
2393 1 1
2394 1 1
2395 2 0
2396 1 1
2397 1 1
2398 1 1
2399 1 1
2400 2 0
2401 1 1
2402 2 0
2403 1 1
2404 2 0
2405 1 1
2406 1 1
2407 1 1
2408 1 1
2409 1 1
2410 1 1
2411 1 1
2412 1 1
2413 1 1
2414 1 1
2415 2 0
2416 1 1
2417 1 1
2418 1 1
2419 2 0
2420 1 1
2421 1 1
2422 3 0
2423 2 0
2424 1 1
2425 1 1
2426 2 0
2427 2 0
2428 1 1
2429 1 1
2430 1 1
2431 1 1
2432 1 1
2433 1 1
2434 1 1
2435 1 1
2436 1 1
2437 1 1
2438 1 1
2439 1 1
2440 1 1
2441 1 1
2442 2 0
2443 1 1
2444 1 1
2445 2 0
2446 3 0
2447 1 1
2448 1 1
2449 2 0
2450 1 1
2451 1 1
2452 1 1
2453 1 1
2454 1 1
2455 1 1
2456 2 0
2457 1 1
2458 1 1
2459 2 0
2460 1 1
2461 1 1
2462 2 0
2463 2 0
2464 1 1
2465 1 1
2466 1 1
2467 1 1
2468 2 0
2469 1 1
2470 2 0
2471 1 1
2472 1 1
2473 1 1
2474 2 0
2475 2 0
2476 2 0
2477 2 0
2478 1 1
2479 1 1
2480 1 1
2481 1 1
2482 1 1
2483 1 1
2484 1 1
2485 1 1
2486 1 1
2487 1 1
2488 1 1
2489 1 1
2490 1 1
2491 1 1
2492 2 0
2493 1 1
2494 1 1
2495 1 1
2496 1 1
2497 1 1
2498 1 1
2499 1 1
2500 1 1
2501 2 0
2502 1 1
2503 1 1
2504 1 1
2505 1 1
2506 1 1
2507 1 1
2508 1 1
2509 1 1
2510 1 1
2511 1 1
2512 2 0
2513 2 0
2514 1 1
2515 1 1
2516 1 1
2517 2 0
2518 2 0
2519 2 0
2520 2 0
2521 2 0
2522 1 1
2523 1 1
2524 1 1
2525 2 0
2526 1 1
2527 1 1
2528 1 1
2529 1 1
2530 2 0
2531 1 1
2532 2 0
2533 1 1
2534 1 1
2535 1 1
2536 1 1
2537 1 1
2538 1 1
2539 1 1
2540 2 0
2541 2 0
2542 2 0
2543 2 0
2544 1 1
2545 1 1
2546 1 1
2547 1 1
2548 1 1
2549 1 1
2550 1 1
2551 2 0
2552 2 0
2553 3 0
2554 1 1
2555 1 1
2556 2 0
2557 1 1
2558 2 0
2559 1 1
2560 1 1
2561 1 1
2562 2 0
2563 1 1
2564 1 1
2565 1 1
2566 1 1
2567 1 1
2568 1 1
2569 1 1
2570 1 1
2571 1 1
2572 1 1
2573 1 1
2574 3 0
2575 1 1
2576 1 1
2577 1 1
2578 1 1
2579 1 1
2580 1 1
2581 1 1
2582 1 1
2583 1 1
2584 1 1
2585 1 1
2586 1 1
2587 1 1
2588 2 0
2589 1 1
2590 1 1
2591 2 0
2592 1 1
2593 1 1
2594 1 1
2595 1 1
2596 1 1
2597 1 1
2598 1 1
2599 1 1
2600 1 1
2601 1 1
2602 1 1
2603 2 0
2604 1 1
2605 2 0
2606 1 1
2607 2 0
2608 1 1
2609 1 1
2610 1 1
2611 1 1
2612 2 0
2613 2 0
2614 1 1
2615 1 1
2616 2 0
2617 1 1
2618 1 1
2619 1 1
2620 1 1
2621 3 0
2622 1 1
2623 1 1
2624 2 0
2625 1 1
2626 3 0
2627 1 1
2628 1 1
2629 1 1
2630 1 1
2631 1 1
2632 1 1
2633 1 1
2634 1 1
2635 1 1
2636 1 1
2637 1 1
2638 1 1
2639 1 1
2640 1 1
2641 1 1
2642 2 0
2643 1 1
2644 1 1
2645 1 1
2646 1 1
2647 1 1
2648 1 1
2649 1 1
2650 1 1
2651 1 1
2652 1 1
2653 1 1
2654 1 1
2655 1 1
2656 1 1
2657 1 1
2658 1 1
2659 1 1
2660 3 0
2661 3 0
2662 1 1
2663 1 1
2664 2 0
2665 3 0
2666 1 1
2667 1 1
2668 1 1
2669 1 1
2670 1 1
2671 1 1
2672 1 1
2673 1 1
2674 1 1
2675 2 0
2676 2 0
2677 1 1
2678 1 1
2679 2 0
2680 2 0
2681 3 0
2682 1 1
2683 2 0
2684 1 1
2685 2 0
2686 2 0
2687 2 0
2688 1 1
2689 2 0
2690 1 1
2691 2 0
2692 2 0
2693 1 1
2694 2 0
2695 2 0
2696 2 0
2697 2 0
2698 3 0
2699 1 1
2700 2 0
2701 1 1
2702 2 0
2703 1 1
2704 3 0
2705 1 1
2706 3 0
2707 1 1
2708 1 1
2709 1 1
2710 1 1
2711 2 0
2712 2 0
2713 2 0
2714 1 1
2715 1 1
2716 2 0
2717 1 1
2718 2 0
2719 1 1
2720 1 1
2721 1 1
2722 2 0
2723 3 0
2724 1 1
2725 2 0
2726 1 1
2727 2 0
2728 2 0
2729 3 0
2730 1 1
2731 3 0
2732 1 1
2733 1 1
2734 1 1
2735 1 1
2736 1 1
2737 1 1
2738 1 1
2739 3 0
2740 1 1
2741 1 1
2742 1 1
2743 1 1
2744 1 1
2745 2 0
2746 1 1
2747 1 1
2748 1 1
2749 1 1
2750 1 1
2751 1 1
2752 1 1
2753 1 1
2754 1 1
2755 2 0
2756 1 1
2757 2 0
2758 1 1
2759 2 0
2760 3 0
2761 2 0
2762 1 1
2763 2 0
2764 1 1
2765 1 1
2766 2 0
2767 2 0
2768 1 1
2769 1 1
2770 2 0
2771 1 1
2772 1 1
2773 1 1
2774 1 1
2775 1 1
2776 1 1
2777 2 0
2778 2 0
2779 1 1
2780 1 1
2781 1 1
2782 2 0
2783 1 1
2784 1 1
2785 1 1
2786 1 1
2787 1 1
2788 1 1
2789 1 1
2790 1 1
2791 1 1
2792 1 1
2793 1 1
2794 1 1
2795 1 1
2796 1 1
2797 1 1
2798 1 1
2799 1 1
2800 3 0
2801 1 1
2802 2 0
2803 1 1
2804 1 1
2805 1 1
2806 1 1
2807 1 1
2808 3 0
2809 2 0
2810 1 1
2811 1 1
2812 2 0
2813 2 0
2814 1 1
2815 1 1
2816 1 1
2817 1 1
2818 1 1
2819 1 1
2820 3 0
2821 2 0
2822 3 0
2823 2 0
2824 1 1
2825 2 0
2826 2 0
2827 1 1
2828 2 0
2829 2 0
2830 1 1
2831 3 0
2832 2 0
2833 3 0
2834 1 1
2835 2 0
2836 3 0
2837 1 1
2838 1 1
2839 1 1
2840 3 0
2841 1 1
2842 3 0
2843 1 1
2844 1 1
2845 1 1
2846 2 0
2847 1 1
2848 1 1
2849 2 0
2850 1 1
2851 1 1
2852 2 0
2853 2 0
2854 3 0
2855 2 0
2856 3 0
2857 1 1
2858 1 1
2859 3 0
2860 2 0
2861 3 0
2862 1 1
2863 2 0
2864 3 0
2865 1 1
2866 1 1
2867 1 1
2868 1 1
2869 3 0
2870 2 0
2871 1 1
2872 1 1
2873 1 1
2874 1 1
2875 1 1
2876 1 1
2877 1 1
2878 1 1
2879 2 0
2880 3 0
2881 1 1
2882 1 1
2883 2 0
2884 1 1
2885 2 0
2886 2 0
2887 1 1
2888 1 1
2889 2 0
2890 1 1
2891 1 1
2892 1 1
2893 1 1
2894 1 1
2895 1 1
2896 1 1
2897 1 1
2898 1 1
2899 2 0
2900 1 1
2901 1 1
2902 1 1
2903 2 0
2904 1 1
2905 1 1
2906 3 0
2907 1 1
2908 1 1
2909 2 0
2910 1 1
2911 1 1
2912 1 1
2913 1 1
2914 2 0
2915 1 1
2916 1 1
2917 2 0
2918 1 1
2919 1 1
2920 1 1
2921 1 1
2922 1 1
2923 1 1
2924 1 1
2925 1 1
2926 1 1
2927 2 0
2928 1 1
2929 1 1
2930 2 0
2931 1 1
2932 1 1
2933 1 1
2934 1 1
2935 1 1
2936 1 1
2937 1 1
2938 1 1
2939 1 1
2940 2 0
2941 2 0
2942 2 0
2943 2 0
2944 1 1
2945 1 1
2946 1 1
2947 1 1
2948 1 1
2949 1 1
2950 1 1
2951 1 1
2952 1 1
2953 1 1
2954 1 1
2955 1 1
2956 1 1
2957 1 1
2958 1 1
2959 1 1
2960 1 1
2961 2 0
2962 1 1
2963 1 1
2964 1 1
2965 1 1
2966 1 1
2967 2 0
2968 2 0
2969 2 0
2970 2 0
2971 1 1
2972 1 1
2973 1 1
2974 1 1
2975 1 1
2976 1 1
2977 3 0
2978 1 1
2979 2 0
2980 2 0
2981 1 1
2982 1 1
2983 1 1
2984 1 1
2985 3 0
2986 2 0
2987 1 1
2988 2 0
2989 2 0
2990 1 1
2991 3 0
2992 1 1
2993 1 1
2994 1 1
2995 1 1
2996 1 1
2997 1 1
2998 1 1
2999 1 1
3000 1 1
3001 2 0
3002 1 1
3003 1 1
3004 1 1
3005 1 1
3006 1 1
3007 1 1
3008 1 1
3009 2 0
3010 1 1
3011 1 1
3012 2 0
3013 1 1
3014 1 1
3015 2 0
3016 1 1
3017 1 1
3018 2 0
3019 2 0
3020 1 1
3021 1 1
3022 1 1
3023 1 1
3024 1 1
3025 1 1
3026 1 1
3027 1 1
3028 1 1
3029 1 1
3030 1 1
3031 1 1
3032 2 0
3033 1 1
3034 1 1
3035 1 1
3036 1 1
3037 1 1
3038 2 0
3039 2 0
3040 2 0
3041 2 0
3042 3 0
3043 1 1
3044 2 0
3045 2 0
3046 1 1
3047 1 1
3048 1 1
3049 1 1
3050 2 0
3051 1 1
3052 2 0
3053 2 0
3054 1 1
3055 1 1
3056 2 0
3057 1 1
3058 1 1
3059 1 1
3060 1 1
3061 2 0
3062 1 1
3063 1 1
3064 1 1
3065 2 0
3066 2 0
3067 2 0
3068 1 1
3069 2 0
3070 1 1
3071 1 1
3072 1 1
3073 1 1
3074 2 0
3075 1 1
3076 1 1
3077 1 1
3078 1 1
3079 1 1
3080 1 1
3081 1 1
3082 1 1
3083 1 1
3084 1 1
3085 1 1
3086 1 1
3087 2 0
3088 1 1
3089 1 1
3090 1 1
3091 1 1
3092 2 0
3093 2 0
3094 1 1
3095 2 0
3096 1 1
3097 2 0
3098 1 1
3099 1 1
3100 1 1
3101 2 0
3102 1 1
3103 1 1
3104 1 1
3105 1 1
3106 1 1
3107 1 1
3108 1 1
3109 1 1
3110 2 0
3111 2 0
3112 2 0
3113 1 1
3114 1 1
3115 2 0
3116 3 0
3117 1 1
3118 2 0
3119 1 1
3120 2 0
3121 2 0
3122 1 1
3123 1 1
3124 2 0
3125 1 1
3126 2 0
3127 1 1
3128 1 1
3129 1 1
3130 1 1
3131 1 1
3132 1 1
3133 1 1
3134 1 1
3135 2 0
3136 1 1
3137 1 1
3138 1 1
3139 1 1
3140 1 1
3141 2 0
3142 1 1
3143 1 1
3144 1 1
3145 1 1
3146 1 1
3147 1 1
3148 1 1
3149 1 1
3150 2 0
3151 1 1
3152 1 1
3153 1 1
3154 1 1
3155 1 1
3156 1 1
3157 1 1
3158 1 1
3159 1 1
3160 1 1
3161 1 1
3162 2 0
3163 1 1
3164 1 1
3165 1 1
3166 1 1
3167 1 1
3168 1 1
3169 1 1
3170 1 1
3171 1 1
3172 1 1
3173 1 1
3174 1 1
3175 1 1
3176 1 1
3177 1 1
3178 2 0
3179 1 1
3180 1 1
3181 1 1
3182 1 1
3183 2 0
3184 2 0
3185 2 0
3186 1 1
3187 1 1
3188 1 1
3189 2 0
3190 1 1
3191 1 1
3192 1 1
3193 1 1
3194 1 1
3195 2 0
3196 1 1
3197 1 1
3198 1 1
3199 1 1
3200 1 1
3201 3 0
3202 1 1
3203 1 1
3204 1 1
3205 1 1
3206 2 0
3207 1 1
3208 3 0
3209 1 1
3210 1 1
3211 1 1
3212 2 0
3213 2 0
3214 2 0
3215 1 1
3216 1 1
3217 1 1
3218 1 1
3219 1 1
3220 1 1
3221 1 1
3222 2 0
3223 1 1
3224 2 0
3225 1 1
3226 1 1
3227 1 1
3228 2 0
3229 1 1
3230 1 1
3231 1 1
3232 1 1
3233 2 0
3234 1 1
3235 1 1
3236 1 1
3237 2 0
3238 2 0
3239 1 1
3240 1 1
3241 3 0
3242 1 1
3243 2 0
3244 1 1
3245 1 1
3246 1 1
3247 2 0
3248 2 0
3249 1 1
3250 2 0
3251 1 1
3252 1 1
3253 3 0
3254 2 0
3255 2 0
3256 2 0
3257 2 0
3258 1 1
3259 1 1
3260 2 0
3261 1 1
3262 1 1
3263 1 1
3264 2 0
3265 1 1
3266 1 1
3267 1 1
3268 1 1
3269 2 0
3270 1 1
3271 1 1
3272 1 1
3273 1 1
3274 2 0
3275 2 0
3276 1 1
3277 1 1
3278 2 0
3279 2 0
3280 2 0
3281 1 1
3282 1 1
3283 1 1
3284 1 1
3285 1 1
3286 1 1
3287 1 1
3288 1 1
3289 2 0
3290 1 1
3291 1 1
3292 1 1
3293 2 0
3294 1 1
3295 1 1
3296 1 1
3297 1 1
3298 1 1
3299 1 1
3300 1 1
3301 2 0
3302 2 0
3303 1 1
3304 1 1
3305 1 1
3306 1 1
3307 1 1
3308 1 1
3309 1 1
3310 1 1
3311 2 0
3312 1 1
3313 1 1
3314 1 1
3315 2 0
3316 1 1
3317 1 1
3318 1 1
3319 1 1
3320 1 1
3321 1 1
3322 2 0
3323 1 1
3324 1 1
3325 1 1
3326 1 1
3327 1 1
3328 2 0
3329 1 1
3330 1 1
3331 1 1
3332 1 1
3333 1 1
3334 2 0
3335 1 1
3336 1 1
3337 1 1
3338 1 1
3339 1 1
3340 1 1
3341 3 0
3342 1 1
3343 1 1
3344 1 1
3345 1 1
3346 1 1
3347 1 1
3348 1 1
3349 1 1
3350 1 1
3351 1 1
3352 1 1
3353 3 0
3354 2 0
3355 1 1
3356 1 1
3357 1 1
3358 1 1
3359 2 0
3360 1 1
3361 2 0
3362 2 0
3363 1 1
3364 1 1
3365 3 0
3366 1 1
3367 1 1
3368 1 1
3369 1 1
3370 1 1
3371 1 1
3372 1 1
3373 2 0
3374 2 0
3375 1 1
3376 2 0
3377 2 0
3378 1 1
3379 1 1
3380 1 1
3381 1 1
3382 2 0
3383 1 1
3384 1 1
3385 1 1
3386 3 0
3387 1 1
3388 1 1
3389 1 1
3390 2 0
3391 1 1
3392 1 1
3393 1 1
3394 2 0
3395 1 1
3396 1 1
3397 1 1
3398 1 1
3399 1 1
3400 1 1
3401 1 1
3402 1 1
3403 1 1
3404 1 1
3405 1 1
3406 1 1
3407 1 1
3408 1 1
3409 1 1
3410 3 0
3411 2 0
3412 1 1
3413 1 1
3414 1 1
3415 1 1
3416 1 1
3417 1 1
3418 1 1
3419 1 1
3420 3 0
3421 1 1
3422 1 1
3423 2 0
3424 1 1
3425 1 1
3426 1 1
3427 1 1
3428 1 1
3429 1 1
3430 1 1
3431 1 1
3432 1 1
3433 2 0
3434 1 1
3435 1 1
3436 1 1
3437 1 1
3438 1 1
3439 2 0
3440 1 1
3441 1 1
3442 1 1
3443 1 1
3444 1 1
3445 1 1
3446 1 1
3447 1 1
3448 1 1
3449 1 1
3450 1 1
3451 1 1
3452 1 1
3453 2 0
3454 1 1
3455 1 1
3456 1 1
3457 1 1
3458 1 1
3459 1 1
3460 2 0
3461 2 0
3462 1 1
3463 2 0
3464 1 1
3465 1 1
3466 1 1
3467 1 1
3468 2 0
3469 1 1
3470 1 1
3471 1 1
3472 1 1
3473 2 0
3474 2 0
3475 1 1
3476 1 1
3477 1 1
3478 1 1
3479 1 1
3480 1 1
3481 2 0
3482 2 0
3483 1 1
3484 2 0
3485 3 0
3486 1 1
3487 1 1
3488 1 1
3489 1 1
3490 1 1
3491 1 1
3492 2 0
3493 1 1
3494 1 1
3495 3 0
3496 2 0
3497 1 1
3498 1 1
3499 1 1
3500 1 1
3501 2 0
3502 1 1
3503 1 1
3504 1 1
3505 2 0
3506 3 0
3507 2 0
3508 1 1
3509 1 1
3510 1 1
3511 1 1
3512 1 1
3513 1 1
3514 1 1
3515 2 0
3516 1 1
3517 1 1
3518 1 1
3519 1 1
3520 3 0
3521 1 1
3522 1 1
3523 1 1
3524 2 0
3525 1 1
3526 1 1
3527 2 0
3528 1 1
3529 1 1
3530 1 1
3531 1 1
3532 1 1
3533 2 0
3534 1 1
3535 3 0
3536 1 1
3537 1 1
3538 1 1
3539 1 1
3540 1 1
3541 2 0
3542 2 0
3543 2 0
3544 1 1
3545 2 0
3546 3 0
3547 1 1
3548 2 0
3549 1 1
3550 1 1
3551 1 1
3552 3 0
3553 3 0
3554 1 1
3555 1 1
3556 1 1
3557 1 1
3558 1 1
3559 1 1
3560 2 0
3561 3 0
3562 1 1
3563 2 0
3564 1 1
3565 1 1
3566 1 1
3567 1 1
3568 1 1
3569 1 1
3570 2 0
3571 1 1
3572 1 1
3573 1 1
3574 1 1
3575 3 0
3576 2 0
3577 1 1
3578 1 1
3579 1 1
3580 1 1
3581 1 1
3582 3 0
3583 1 1
3584 1 1
3585 1 1
3586 1 1
3587 2 0
3588 1 1
3589 1 1
3590 3 0
3591 2 0
3592 1 1
3593 1 1
3594 1 1
3595 1 1
3596 2 0
3597 2 0
3598 1 1
3599 2 0
3600 2 0
3601 1 1
3602 3 0
3603 2 0
3604 1 1
3605 1 1
3606 1 1
3607 1 1
3608 2 0
3609 3 0
3610 1 1
3611 1 1
3612 1 1
3613 1 1
3614 1 1
3615 1 1
3616 1 1
3617 1 1
3618 2 0
3619 1 1
3620 1 1
3621 1 1
3622 2 0
3623 1 1
3624 1 1
3625 1 1
3626 3 0
3627 1 1
3628 1 1
3629 1 1
3630 1 1
3631 1 1
3632 2 0
3633 1 1
3634 3 0
3635 2 0
3636 1 1
3637 1 1
3638 1 1
3639 1 1
3640 3 0
3641 1 1
3642 1 1
3643 1 1
3644 1 1
3645 1 1
3646 1 1
3647 1 1
3648 1 1
3649 1 1
3650 3 0
3651 1 1
3652 3 0
3653 1 1
3654 3 0
3655 1 1
3656 2 0
3657 1 1
3658 1 1
3659 1 1
3660 1 1
3661 3 0
3662 1 1
3663 2 0
3664 2 0
3665 2 0
3666 2 0
3667 1 1
3668 1 1
3669 1 1
3670 2 0
3671 1 1
3672 1 1
3673 1 1
3674 2 0
3675 1 1
3676 1 1
3677 3 0
3678 2 0
3679 1 1
3680 1 1
3681 1 1
3682 2 0
3683 1 1
3684 3 0
3685 1 1
3686 1 1
3687 2 0
3688 1 1
3689 3 0
3690 1 1
3691 3 0
3692 1 1
3693 2 0
3694 1 1
3695 1 1
3696 1 1
3697 1 1
3698 1 1
3699 1 1
3700 3 0
3701 1 1
3702 1 1
3703 1 1
3704 1 1
3705 1 1
3706 1 1
3707 1 1
3708 1 1
3709 1 1
3710 1 1
3711 1 1
3712 1 1
3713 1 1
3714 1 1
3715 3 0
3716 1 1
3717 2 0
3718 1 1
3719 3 0
3720 1 1
3721 1 1
3722 1 1
3723 1 1
3724 2 0
3725 1 1
3726 1 1
3727 1 1
3728 1 1
3729 2 0
3730 3 0
3731 1 1
3732 3 0
3733 1 1
3734 1 1
3735 1 1
3736 1 1
3737 3 0
3738 1 1
3739 1 1
3740 1 1
3741 1 1
3742 1 1
3743 3 0
3744 1 1
3745 1 1
3746 3 0
3747 1 1
3748 1 1
3749 3 0
3750 1 1
3751 1 1
3752 1 1
3753 3 0
3754 2 0
3755 1 1
3756 1 1
3757 1 1
3758 1 1
3759 1 1
3760 2 0
3761 1 1
3762 1 1
3763 1 1
3764 2 0
3765 1 1
3766 2 0
3767 1 1
3768 1 1
3769 2 0
3770 3 0
3771 3 0
3772 2 0
3773 1 1
3774 1 1
3775 1 1
3776 1 1
3777 3 0
3778 2 0
3779 2 0
3780 1 1
3781 3 0
3782 1 1
3783 1 1
3784 1 1
3785 3 0
3786 1 1
3787 1 1
3788 1 1
3789 1 1
3790 1 1
3791 3 0
3792 1 1
3793 2 0
3794 1 1
3795 1 1
3796 1 1
3797 1 1
3798 1 1
3799 1 1
3800 1 1
3801 1 1
3802 2 0
3803 3 0
3804 1 1
3805 2 0
3806 1 1
3807 1 1
3808 1 1
3809 1 1
3810 1 1
3811 1 1
3812 1 1
3813 1 1
3814 1 1
3815 1 1
3816 1 1
3817 2 0
3818 2 0
3819 1 1
3820 1 1
3821 1 1
3822 1 1
3823 3 0
3824 3 0
3825 1 1
3826 1 1
3827 1 1
3828 3 0
3829 1 1
3830 1 1
3831 1 1
3832 2 0
3833 1 1
3834 3 0
3835 3 0
3836 2 0
3837 2 0
3838 1 1
3839 2 0
3840 2 0
3841 1 1
3842 1 1
3843 1 1
3844 2 0
3845 1 1
3846 1 1
3847 1 1
3848 1 1
3849 1 1
3850 1 1
3851 1 1
3852 1 1
3853 2 0
3854 1 1
3855 3 0
3856 2 0
3857 2 0
3858 3 0
3859 1 1
3860 1 1
3861 1 1
3862 2 0
3863 1 1
3864 1 1
3865 1 1
3866 1 1
3867 2 0
3868 1 1
3869 1 1
3870 1 1
3871 1 1
3872 1 1
3873 1 1
3874 1 1
3875 1 1
3876 1 1Which of the following implies i.i.d?
Option 1
Option 3
x0 = sample(gss$vote, size = 1)
x1 = sample(gss$vote, size = 1)
x2 = sample(gss$vote, size = 1)
x3 = sample(gss$vote, size = 1)
x4 = sample(gss$vote, size = 1)
x5 = sample(gss$vote, size = 1)
x6 = sample(gss$vote, size = 1)
x7 = sample(gss$vote, size = 1)
x8 = sample(gss$vote, size = 1)
x9 = sample(gss$vote, size = 1)What happens if i.i.d. does not hold?
Back to illustration
Pretend our data is the population
Population mean
Wait what’s the point of random sampling!?
Finite-sample properties
Increase the number of replicates
Result
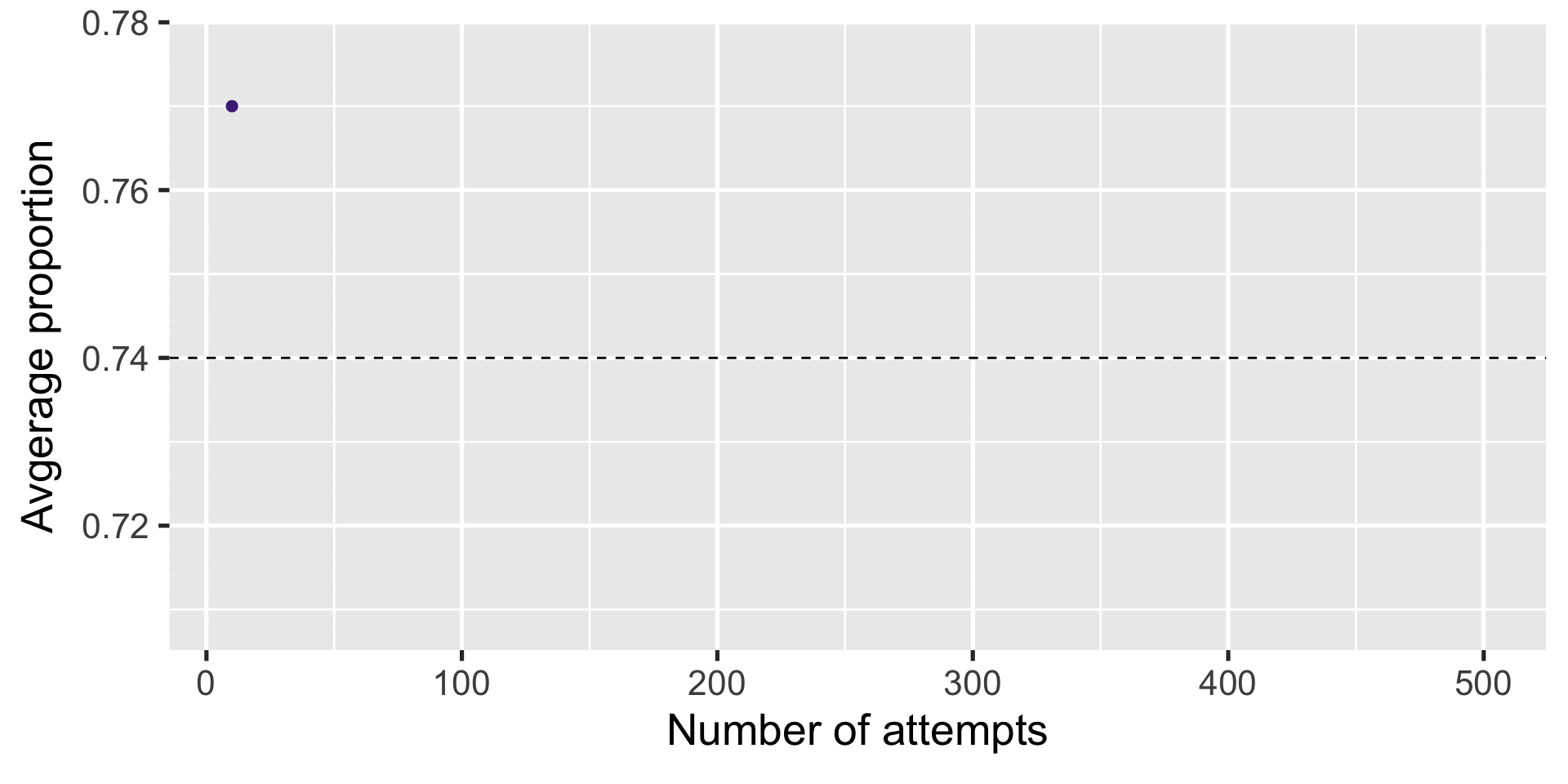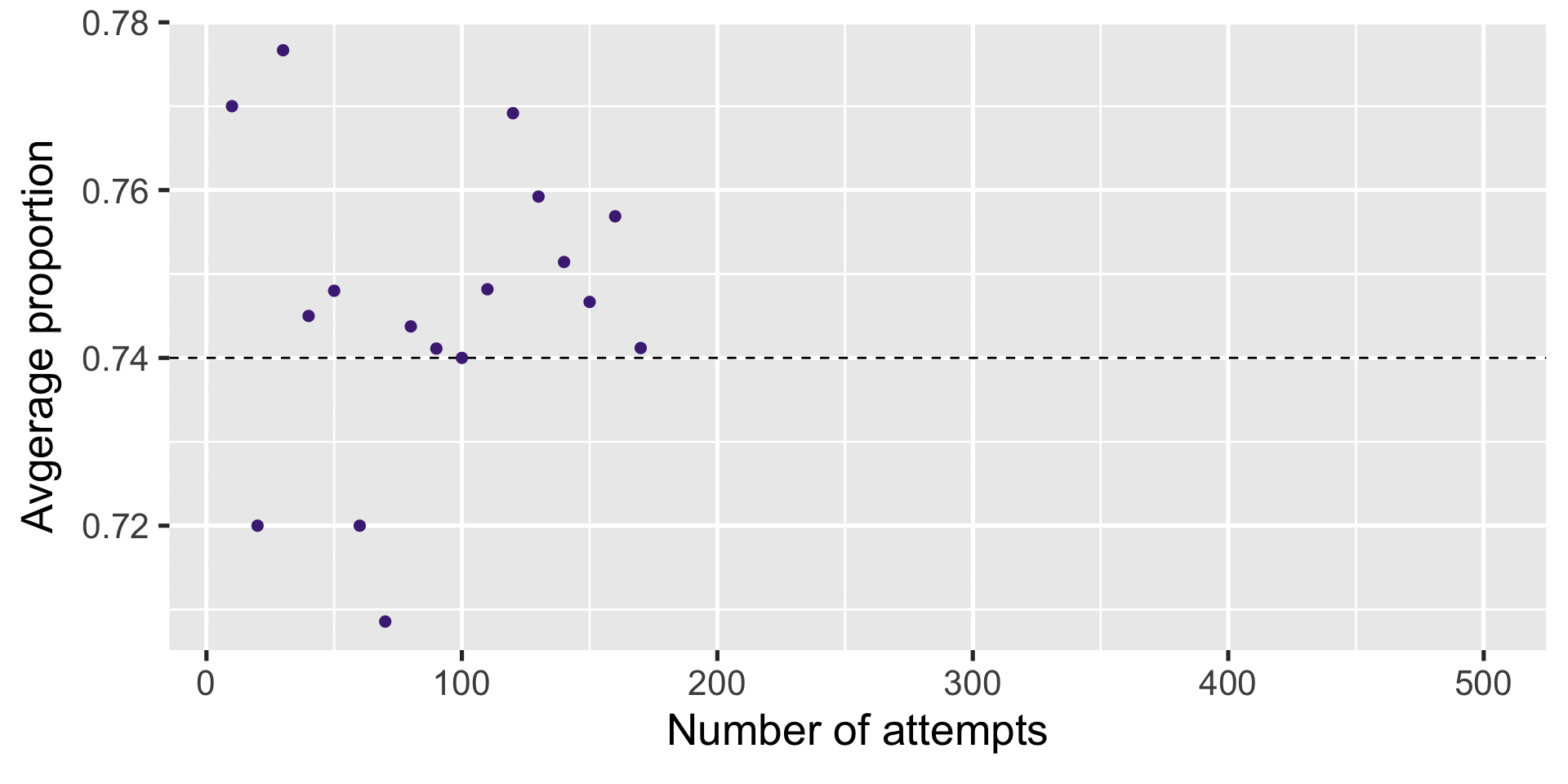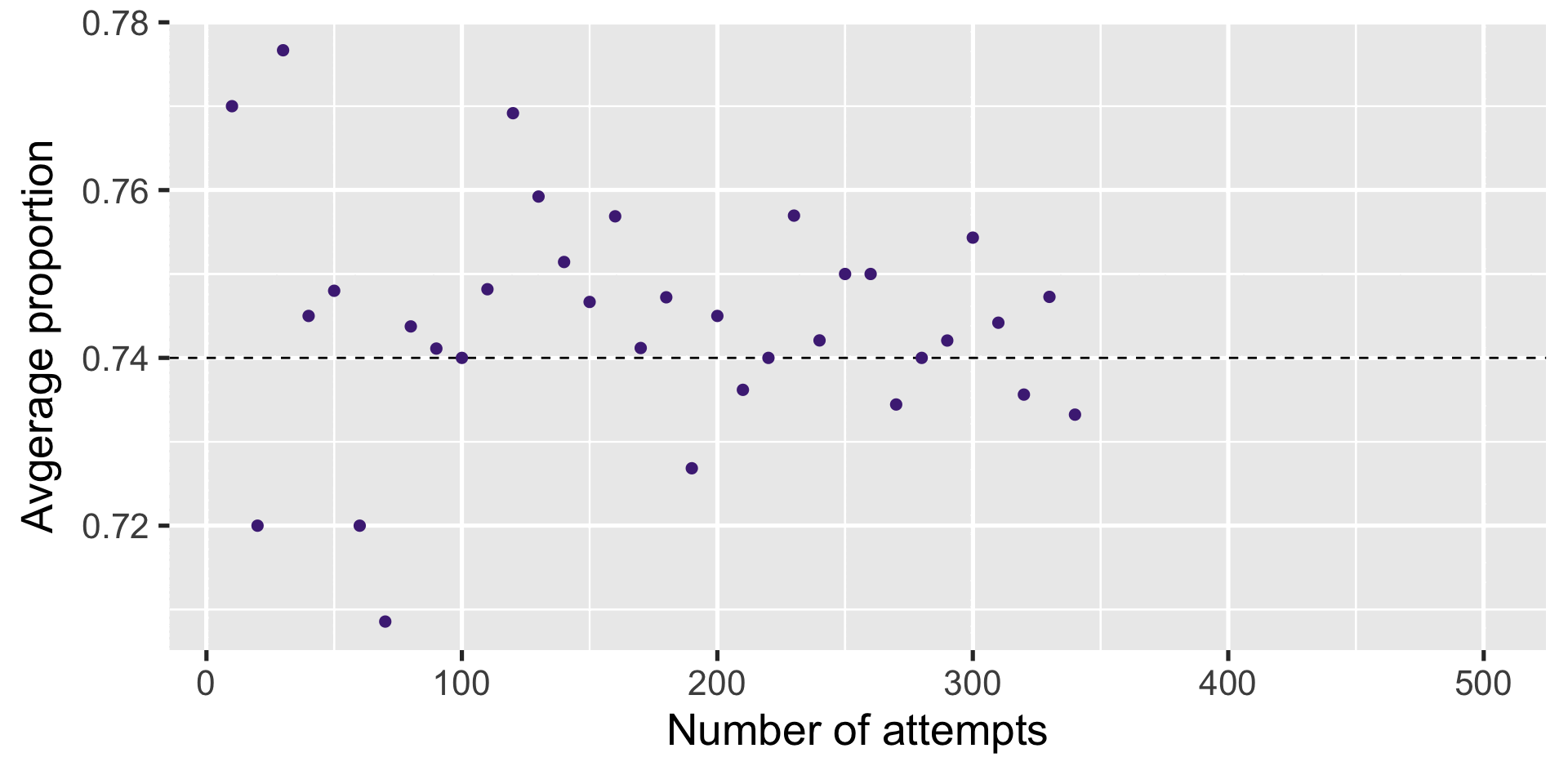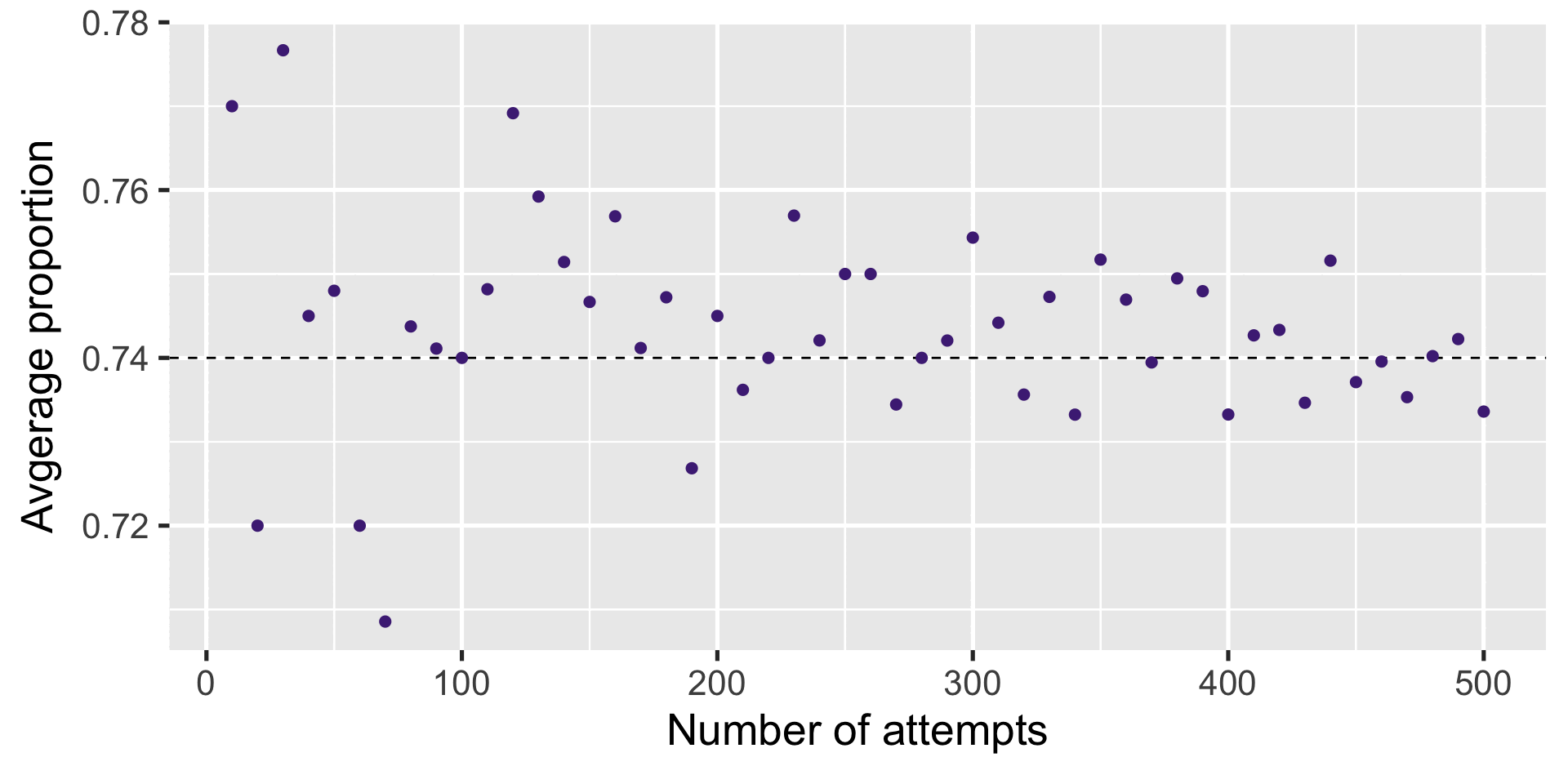
Result
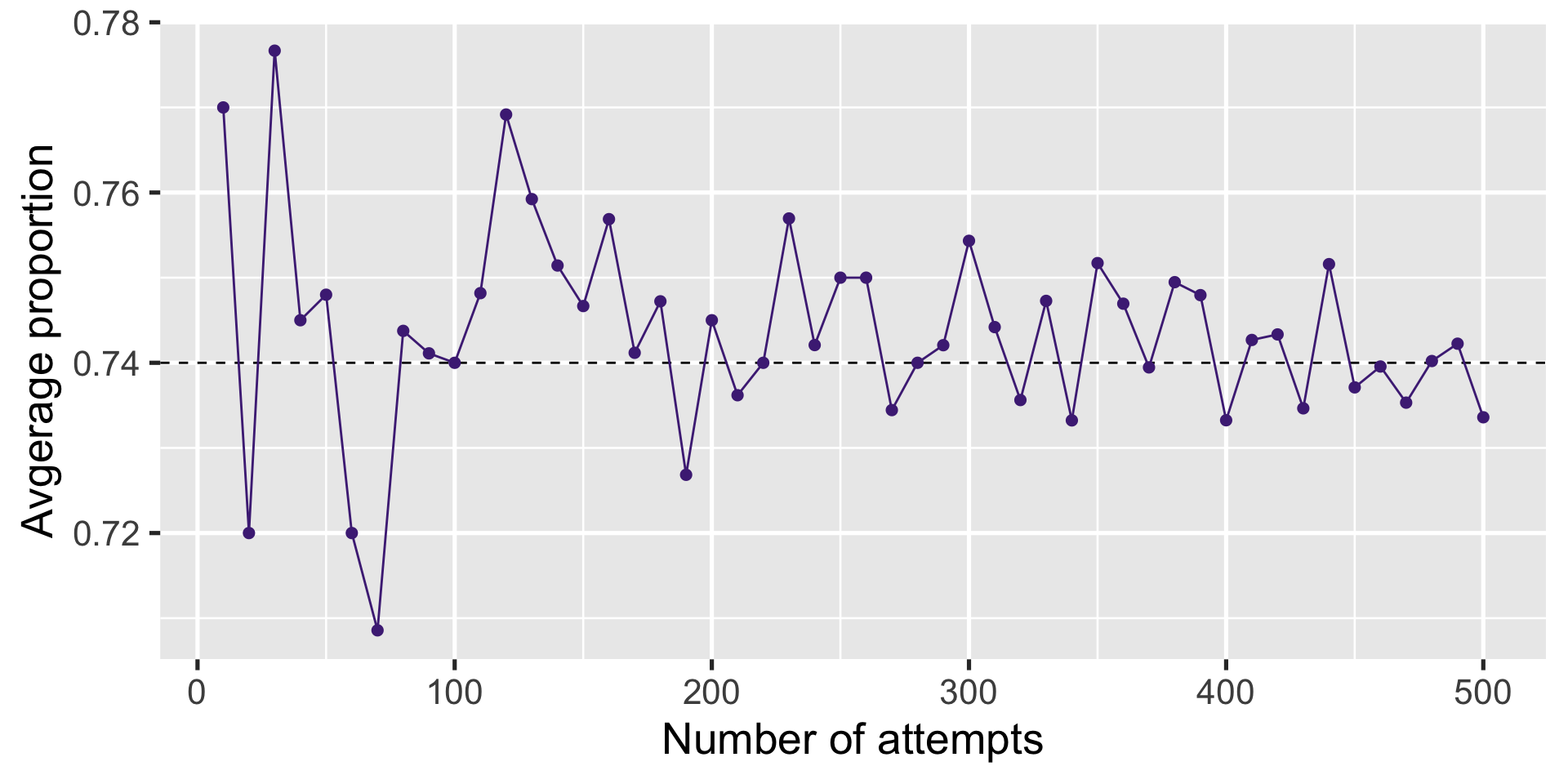
Weak Law of Large Numbers (WLLN)
If you take i.i.d. draws from random variable \(X\) a large number of times
\[ \overline X\xrightarrow{p} E[X] \]
Which implies that the sample mean with a large enough sample size has negligible probability of being far from the true population parameter
Asymptotic properties
n prop
1 10 0.800
2 10 0.700
3 10 1.000
4 10 0.700
5 10 0.800
6 10 0.700
7 10 1.000
8 10 0.700
9 10 0.700
10 10 0.800
11 10 0.600
12 10 0.700
13 10 0.900
14 10 0.700
15 10 0.800
16 10 0.600
17 10 0.900
18 10 0.600
19 10 0.800
20 10 0.500
21 10 0.500
22 10 1.000
23 10 0.900
24 10 0.800
25 10 0.600
26 10 0.600
27 10 0.600
28 10 0.700
29 10 0.800
30 10 0.800
31 10 0.800
32 10 0.900
33 10 0.800
34 10 0.900
35 10 0.800
36 10 0.700
37 10 0.800
38 10 0.900
39 10 0.600
40 10 0.900
41 10 0.800
42 10 0.900
43 10 0.600
44 10 0.700
45 10 0.900
46 10 0.800
47 10 0.700
48 10 0.800
49 10 0.300
50 10 0.800
51 10 0.600
52 10 0.800
53 10 0.600
54 10 0.400
55 10 0.800
56 10 0.600
57 10 0.700
58 10 0.800
59 10 0.600
60 10 0.800
61 10 1.000
62 10 0.700
63 10 0.600
64 10 0.600
65 10 0.700
66 10 0.800
67 10 0.900
68 10 0.700
69 10 0.600
70 10 0.800
71 10 0.800
72 10 0.600
73 10 1.000
74 10 0.600
75 10 0.600
76 10 0.900
77 10 1.000
78 10 0.400
79 10 0.800
80 10 0.600
81 10 0.700
82 10 0.600
83 10 0.700
84 10 0.700
85 10 0.800
86 10 0.900
87 10 0.800
88 10 0.800
89 10 0.800
90 10 0.700
91 10 0.800
92 10 0.600
93 10 0.800
94 10 0.700
95 10 1.000
96 10 0.500
97 10 0.600
98 10 0.600
99 10 0.500
100 10 0.600
101 100 0.730
102 100 0.700
103 100 0.720
104 100 0.760
105 100 0.750
106 100 0.670
107 100 0.780
108 100 0.780
109 100 0.770
110 100 0.750
111 100 0.730
112 100 0.700
113 100 0.730
114 100 0.760
115 100 0.780
116 100 0.810
117 100 0.690
118 100 0.760
119 100 0.750
120 100 0.690
121 100 0.700
122 100 0.770
123 100 0.700
124 100 0.790
125 100 0.800
126 100 0.710
127 100 0.650
128 100 0.780
129 100 0.760
130 100 0.850
131 100 0.850
132 100 0.730
133 100 0.730
134 100 0.770
135 100 0.790
136 100 0.710
137 100 0.830
138 100 0.790
139 100 0.780
140 100 0.690
141 100 0.770
142 100 0.780
143 100 0.750
144 100 0.720
145 100 0.770
146 100 0.730
147 100 0.660
148 100 0.730
149 100 0.740
150 100 0.740
151 100 0.800
152 100 0.760
153 100 0.720
154 100 0.720
155 100 0.770
156 100 0.760
157 100 0.750
158 100 0.790
159 100 0.660
160 100 0.720
161 100 0.780
162 100 0.750
163 100 0.720
164 100 0.730
165 100 0.700
166 100 0.680
167 100 0.740
168 100 0.670
169 100 0.740
170 100 0.650
171 100 0.820
172 100 0.770
173 100 0.700
174 100 0.820
175 100 0.740
176 100 0.720
177 100 0.710
178 100 0.700
179 100 0.730
180 100 0.690
181 100 0.800
182 100 0.730
183 100 0.770
184 100 0.690
185 100 0.720
186 100 0.680
187 100 0.710
188 100 0.720
189 100 0.840
190 100 0.690
191 100 0.750
192 100 0.760
193 100 0.750
194 100 0.810
195 100 0.770
196 100 0.780
197 100 0.790
198 100 0.740
199 100 0.730
200 100 0.800
201 500 0.780
202 500 0.724
203 500 0.732
204 500 0.736
205 500 0.726
206 500 0.732
207 500 0.762
208 500 0.752
209 500 0.766
210 500 0.766
211 500 0.732
212 500 0.744
213 500 0.732
214 500 0.734
215 500 0.762
216 500 0.730
217 500 0.720
218 500 0.766
219 500 0.716
220 500 0.724
221 500 0.706
222 500 0.752
223 500 0.726
224 500 0.724
225 500 0.734
226 500 0.742
227 500 0.766
228 500 0.760
229 500 0.710
230 500 0.724
231 500 0.748
232 500 0.754
233 500 0.716
234 500 0.710
235 500 0.762
236 500 0.708
237 500 0.738
238 500 0.750
239 500 0.724
240 500 0.746
241 500 0.736
242 500 0.760
243 500 0.724
244 500 0.702
245 500 0.712
246 500 0.750
247 500 0.758
248 500 0.752
249 500 0.748
250 500 0.734
251 500 0.764
252 500 0.732
253 500 0.722
254 500 0.742
255 500 0.748
256 500 0.750
257 500 0.778
258 500 0.726
259 500 0.740
260 500 0.744
261 500 0.728
262 500 0.702
263 500 0.770
264 500 0.746
265 500 0.720
266 500 0.740
267 500 0.722
268 500 0.774
269 500 0.744
270 500 0.750
271 500 0.762
272 500 0.732
273 500 0.742
274 500 0.746
275 500 0.732
276 500 0.708
277 500 0.738
278 500 0.748
279 500 0.768
280 500 0.750
281 500 0.746
282 500 0.774
283 500 0.750
284 500 0.734
285 500 0.734
286 500 0.716
287 500 0.770
288 500 0.750
289 500 0.770
290 500 0.710
291 500 0.758
292 500 0.764
293 500 0.778
294 500 0.730
295 500 0.734
296 500 0.740
297 500 0.720
298 500 0.712
299 500 0.736
300 500 0.744Result
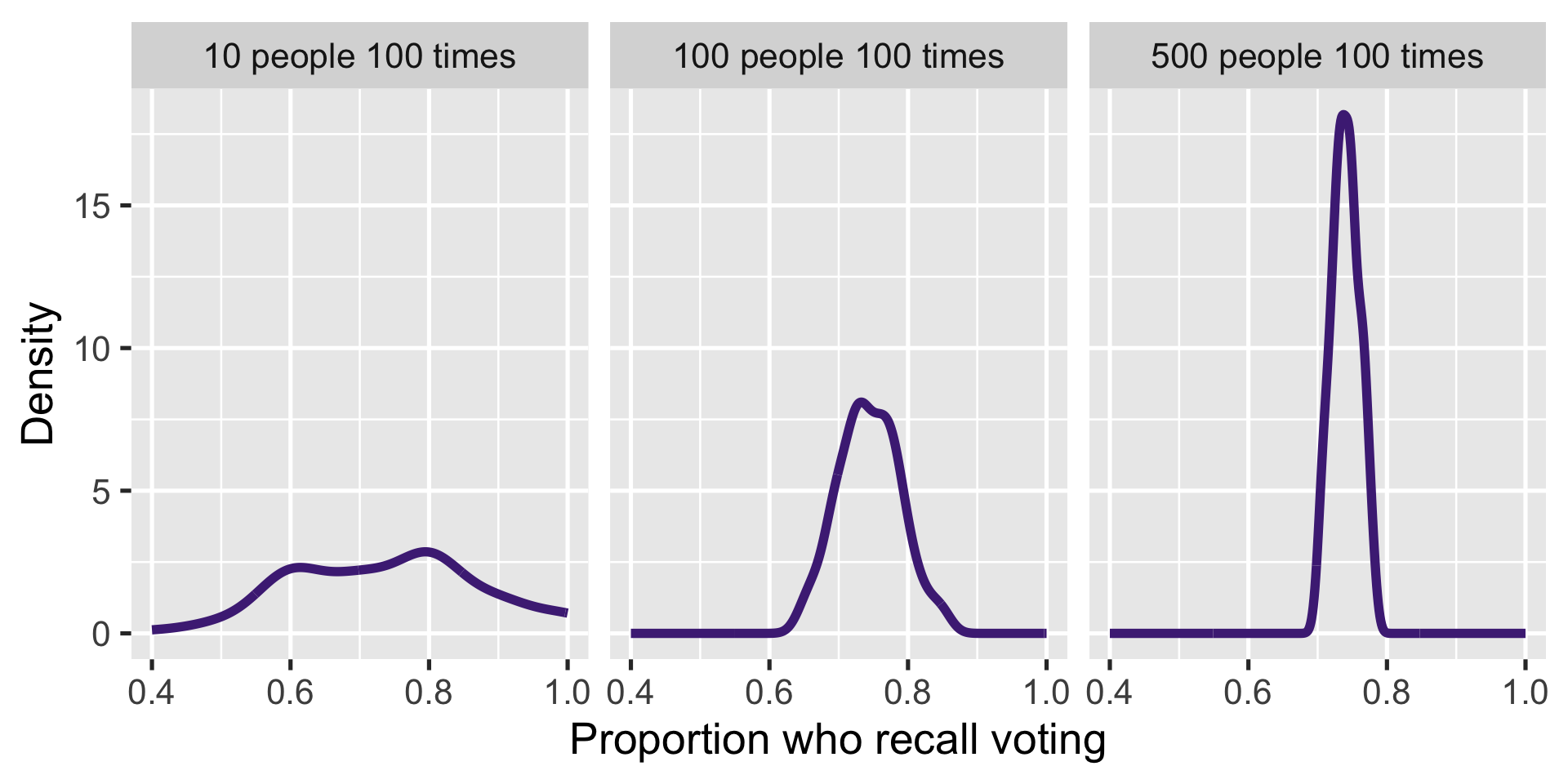
Central limit theorem (CLT)
As sample size increases, the standardized sample mean
\[ Z \xrightarrow{d} N(0,1) \]
where
\[ Z = \frac{(\overline X - E[\overline X])}{\sigma[\overline X]} \]
Central limit theorem (CLT)
As sample size increases, the standardized sample mean
\[ Z \xrightarrow{d} N(0,1) \]
Or without standardizing
\[ \sqrt{n} (\overline X - E[X]) \xrightarrow{d} N(0, \sigma^2) \]
Which implies that if \(n\) is large, then the sample mean will tend to have a normal distribution
Central limit theorem (CLT)
As sample size increases, the standardized sample mean
\[ Z \xrightarrow{d} N(0,1) \]
Or without standardizing
\[ \sqrt{n} (\overline X - E[X]) \xrightarrow{d} N(0, \sigma^2) \]
Which implies that if \(n\) is large, then the sample mean will tend to have a normal distribution even if the population is not distributed normally
Moving on
WLLN and CLT hold for sample means under random sampling
So you do not need to prove them empirically to justify statistical inference
We need additional language to know what happens when they don’t hold
Properties of estimators
Unbiasedness: \(E[\widehat \theta] = \theta\), otherwise biased
Efficiency: \(\widehat \theta_A\) is more efficient than \(\widehat \theta_ B\) if it has lower MSE
Consistency: \(\widehat \theta \overset{p}{\to} \theta\), otherwise inconsistent
Another way to think about it
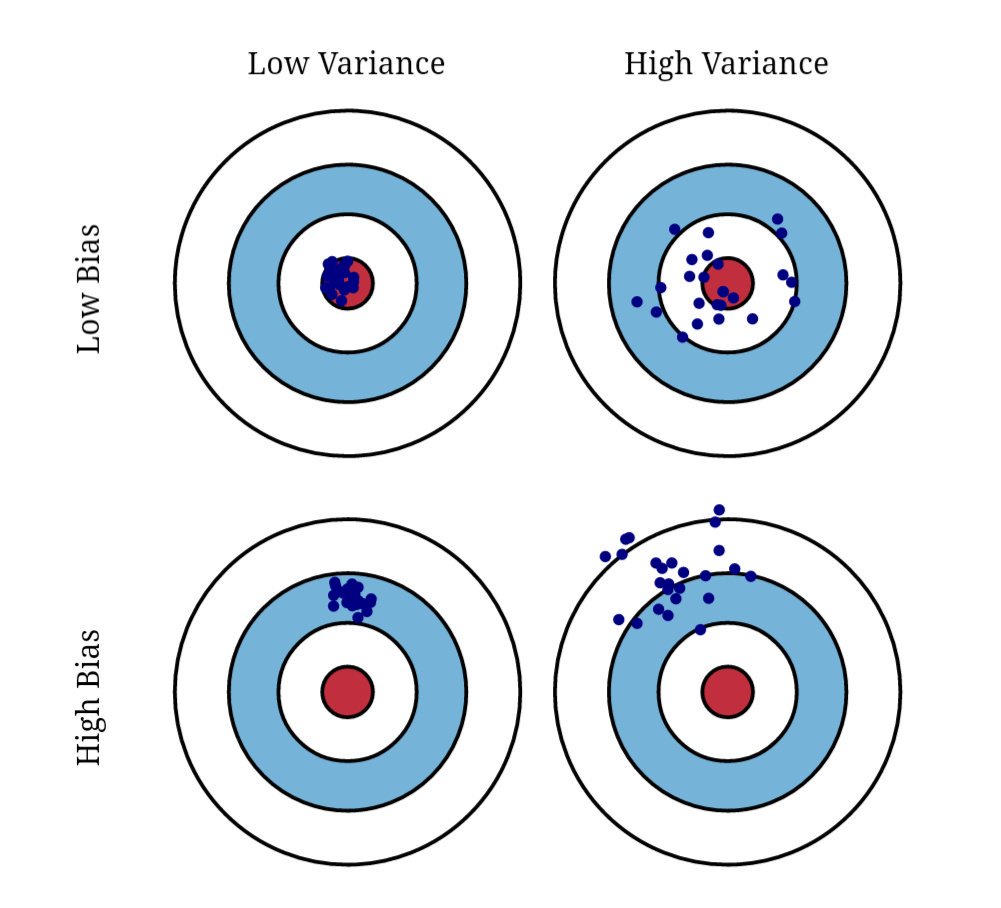
Example: Variance estimation
Why is there a difference?
Hold on
There are two kinds of variance estimators
Sample variance: \(\widehat V[X]\)
Sampling variance: \(V[\overline X]\)
Hold on
There are two kinds of variance estimators
Sample variance: \(\widehat V[X]\) (…of random variable \(X\))
Sampling variance: \(V[\overline X]\) (…of an estimator)
We are talking about sample variance today
Remember: Standard deviation and standard error are different things!
Sample variance estimation
A straightforward candidate from plug-in principle and the alternative formula for variance would be:
\[ \widehat V^*[X] = \overline{X^2} - \overline{X}^2 \]
But it turns out this estimator is biased but consistent
We need to correct the original formula to get an unbiased sample variance
\[ \widehat V[X] = \frac{n}{n-1}(\overline{X^2} - \overline{X}^2) \]
Wrapping up
Random sampling justifies statistical inference via plug-in principle
If this does not hold, we need more theory to connect data to population quantities
In practice, there is always a mismatch between estimates and estimands
Next week: Conveying our uncertainty about the mismatch