Regression

POLI_SCI 403: Probability and Statistics

Agenda

  • Bivariate regression

  • Multivariate regression

  • Inference (lab)

  • Regression with matrix algebra (if we have time)

Bivariate regression

So far

Ingredients for statistical inference

  1. Estimand \(\theta\)

  2. Estimator \(\widehat \theta\)

  3. Data \(X\)

  4. Estimate \(\overline X\)

  5. Quantify uncertainty (confidence intervals, p-values)

\(X \rightarrow \widehat{\theta} \rightarrow \overline{X} \xrightarrow{\text{hopefully!}} \theta\)

MSE and expected value

\[ \text{MSE} = E[(X-\color{purple}c)^2] \]

Alternative formula

\[ \text{MSE} = V[X] + (E[X] - \color{purple}c)^2 \]

\(E[X]\) minimizes MSE

\[ \text{MSE} = V[X] + (E[X] - \color{purple}{E[X]})^2 \]

In practice

This is all about one variable at a time!

We usually want to tell more nuanced stories:

  1. Difference between/across groups
  2. Relationship between two variables
  3. Difference in the relationship between two variables between/across groups

Toy example

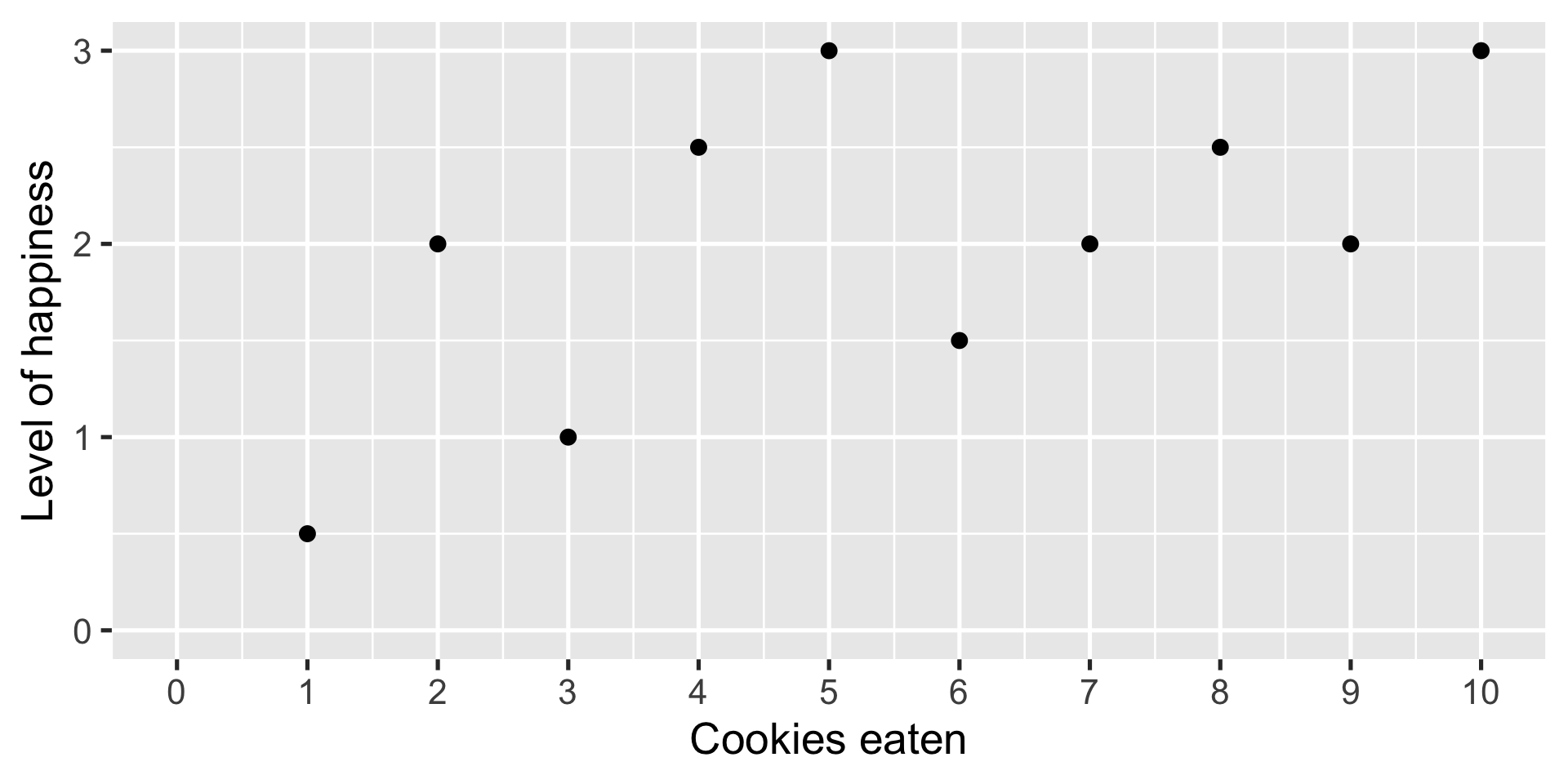
How to summarize?

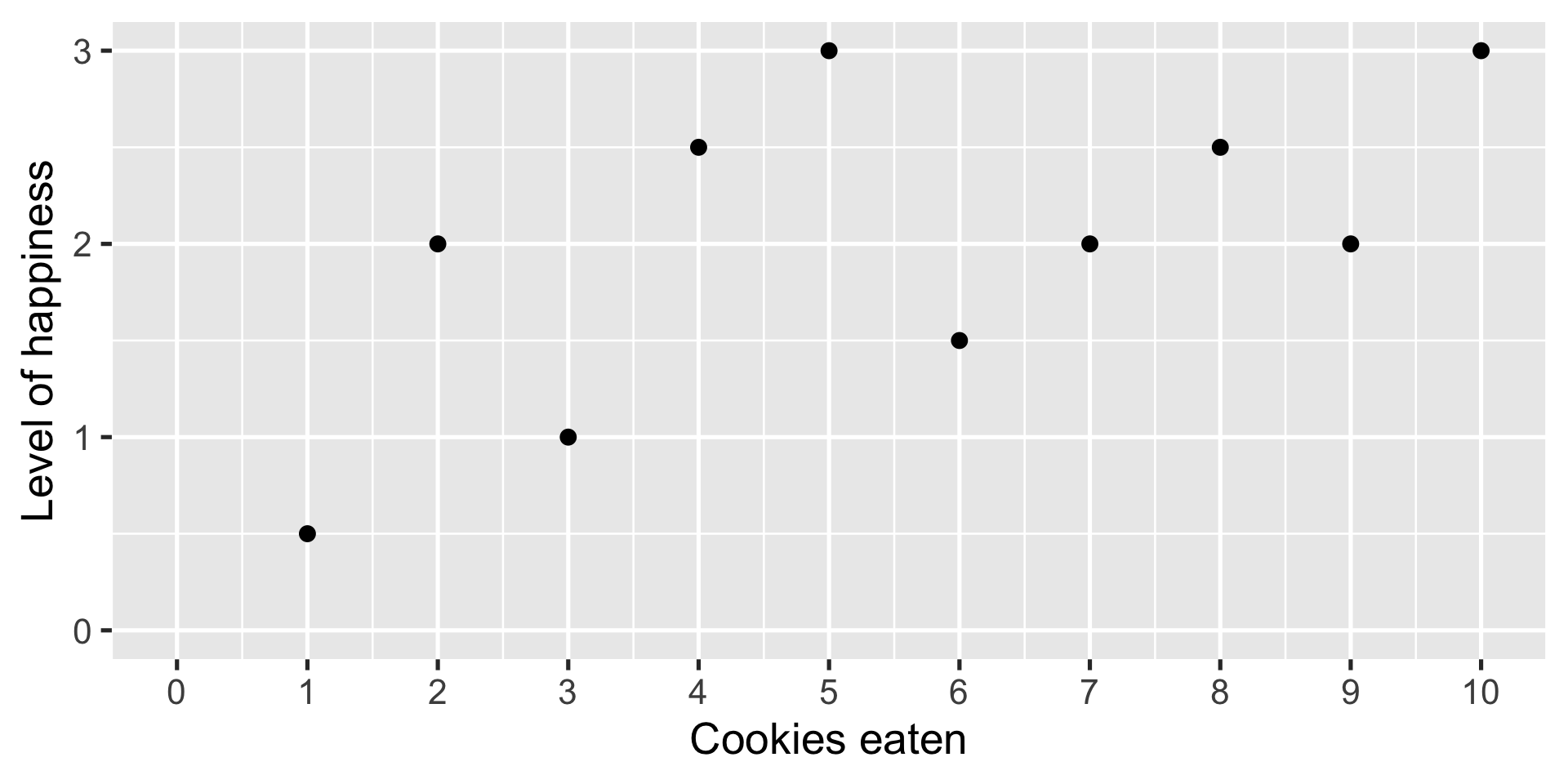
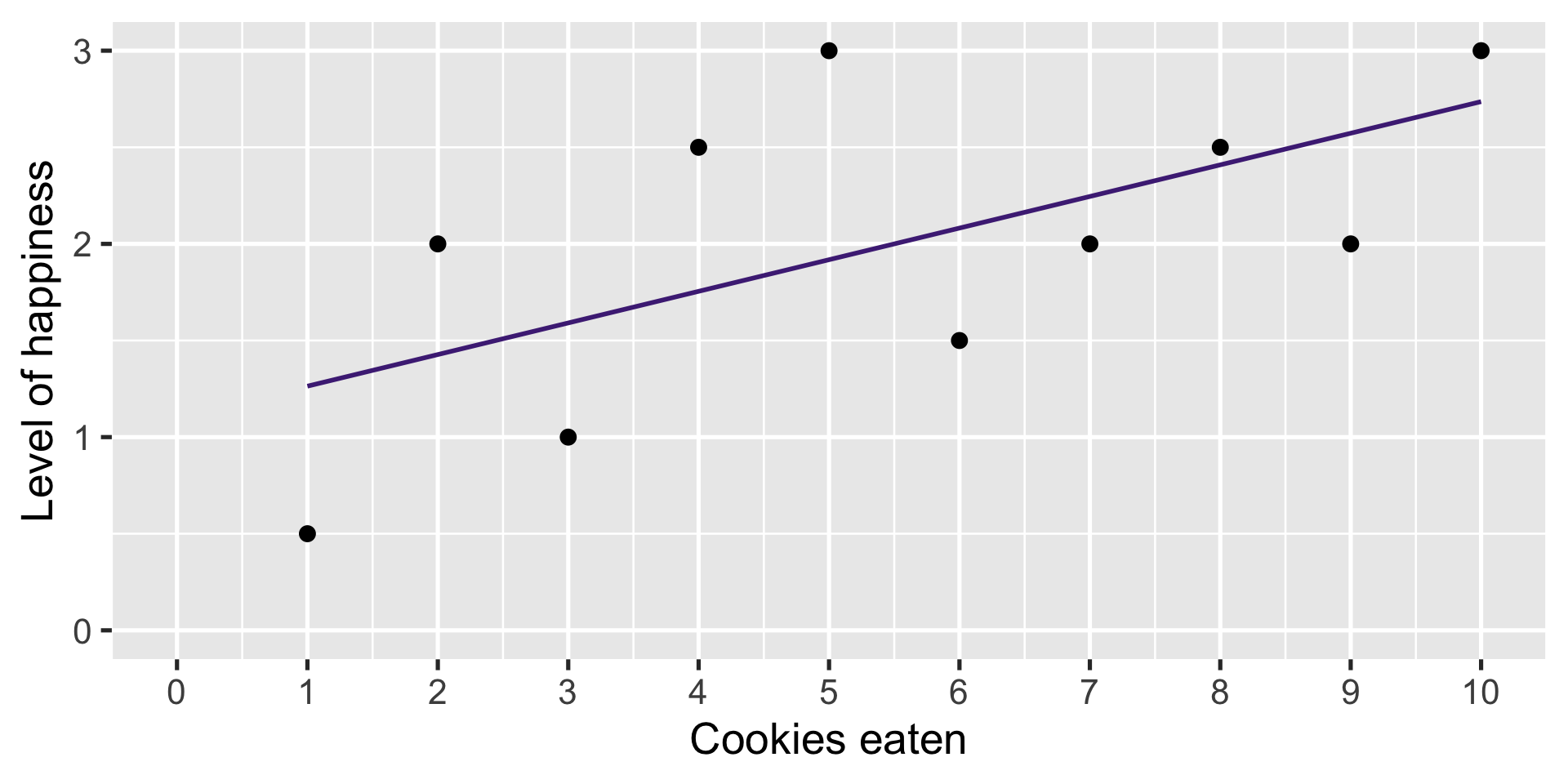
Connect with a line

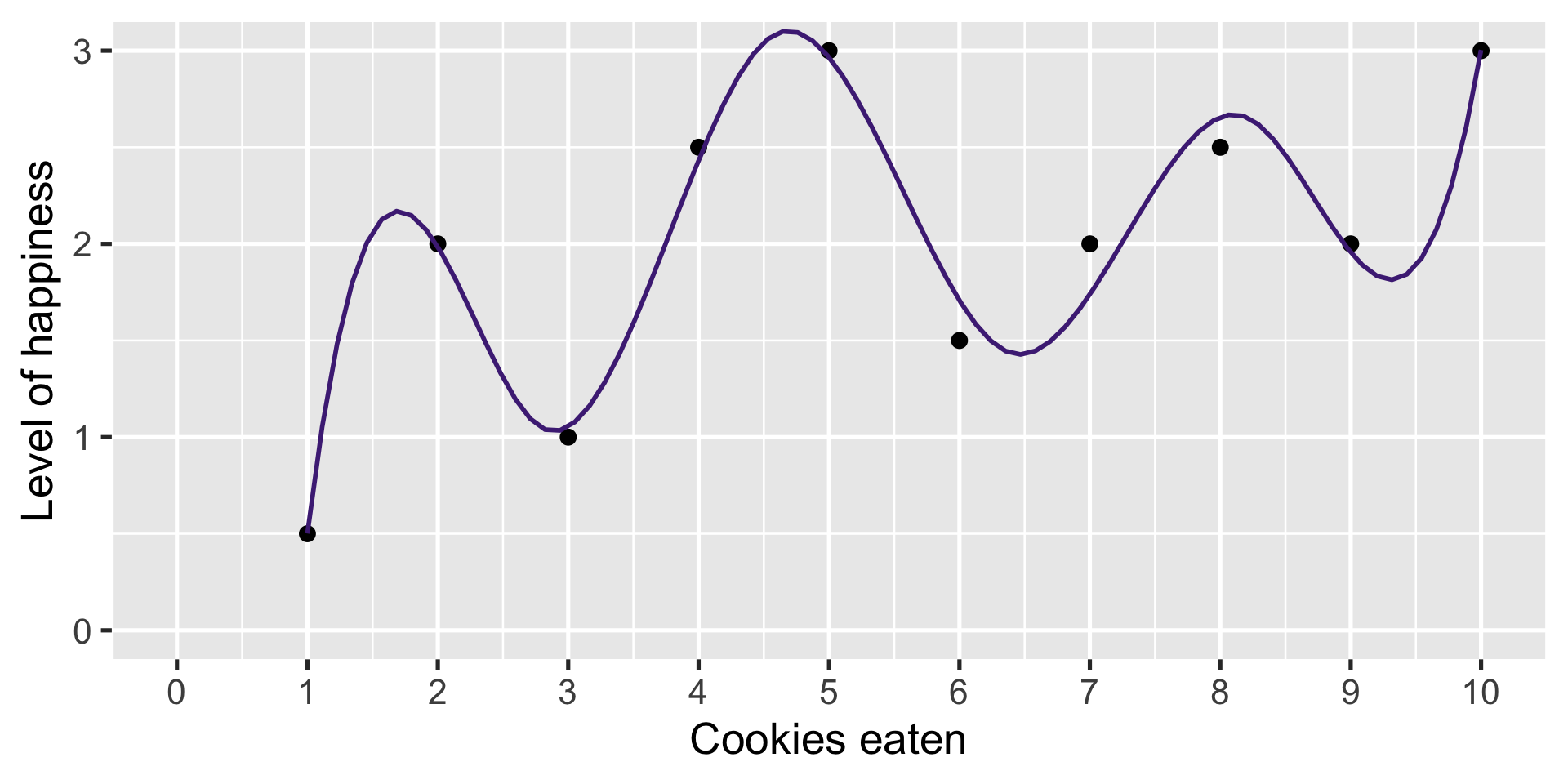
Maybe smoother?

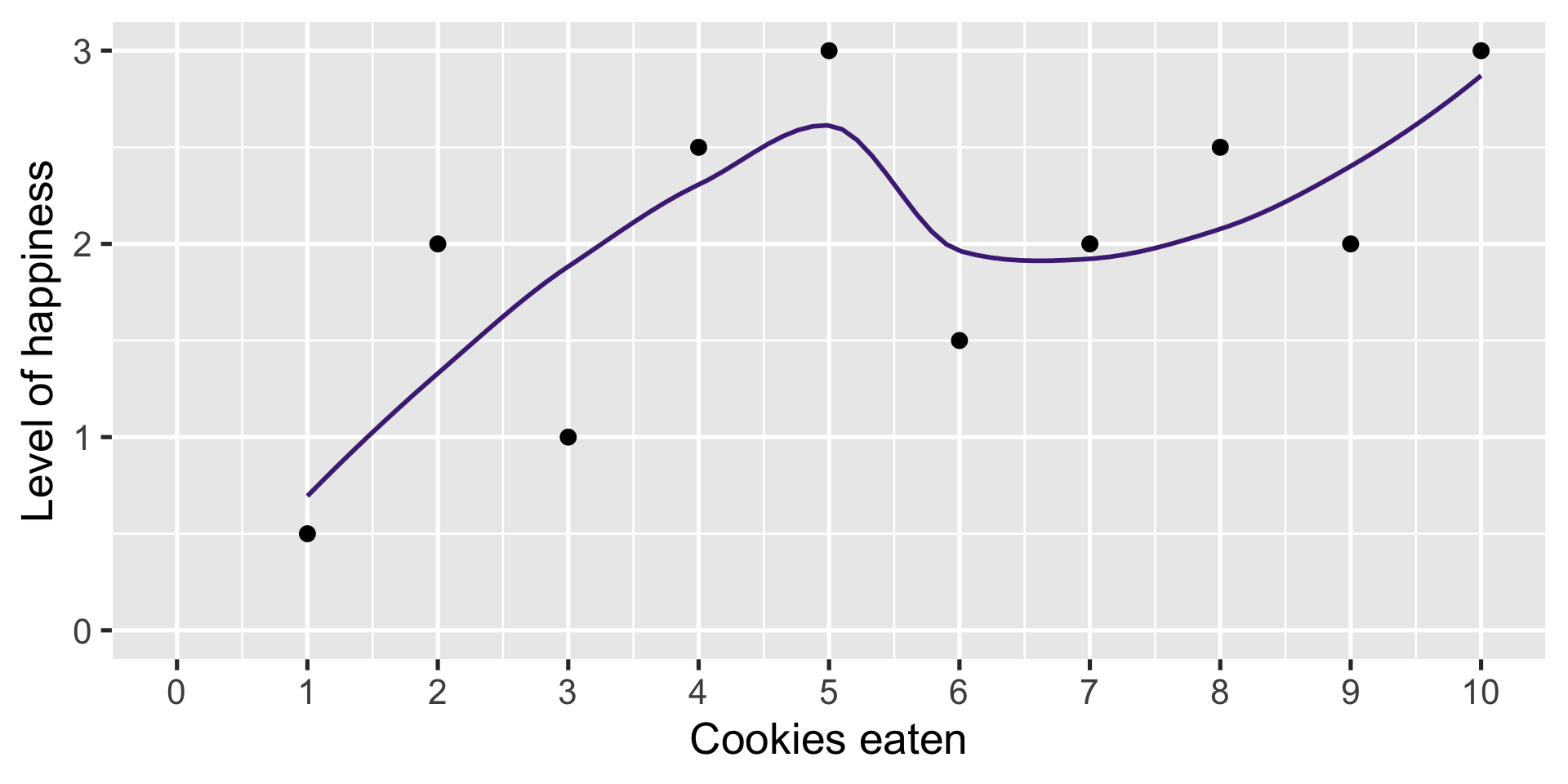
A straight line?

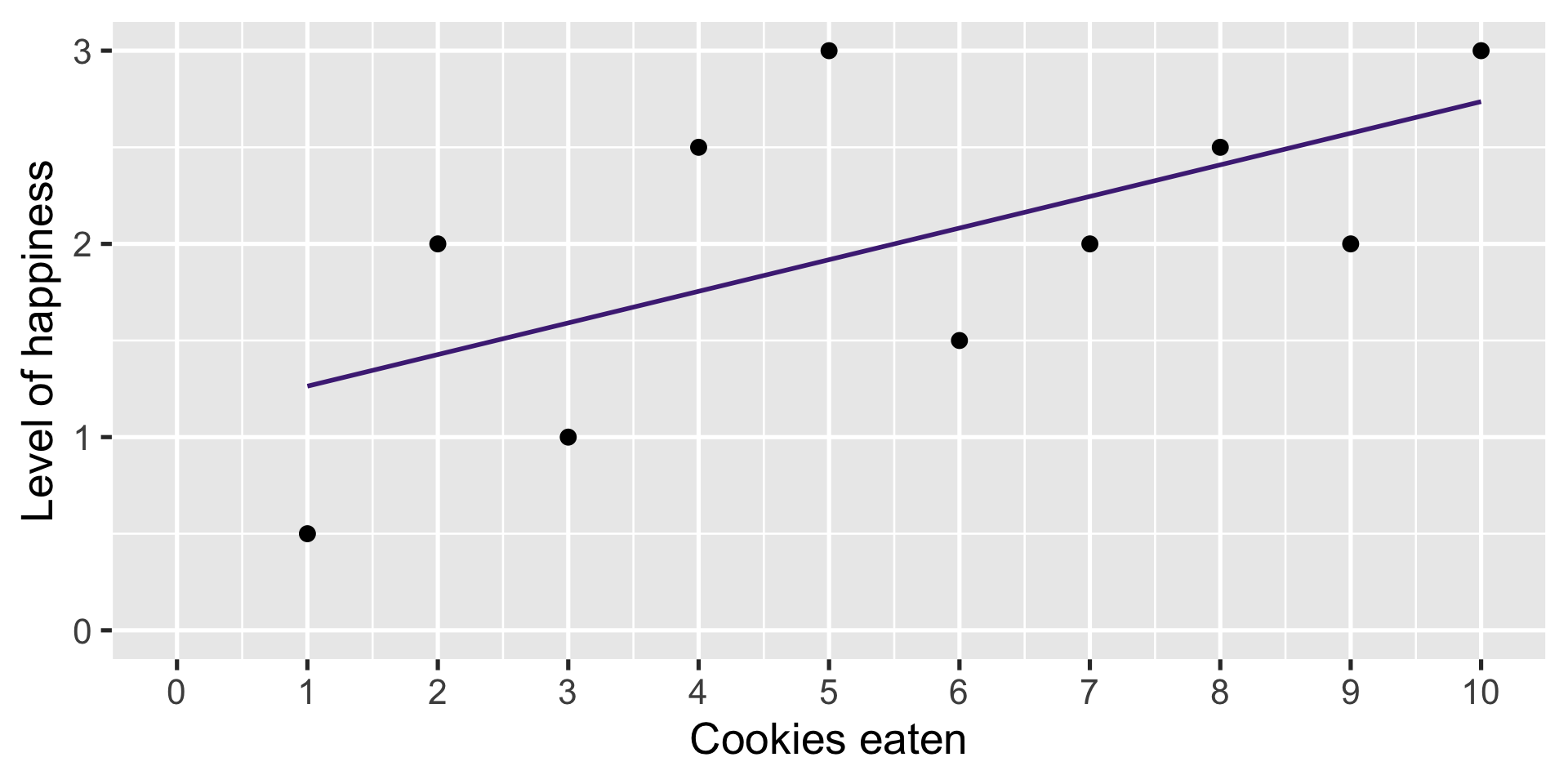
Straight lines are good

They can be written as a linear equation

\[ y = a + bx \]

\(y\)  Outcome variable
\(x\)  Explanatory variable
\(b\)  Slope (\(\frac{\text{rise}}{\text{run}}\))
\(a\)  y-intercept

This is the smallest number of parameters to draw a line

We can think of intercept and slope as estimands

Straight lines are good

They can be written as a linear equation

\[ Y = \alpha + \beta X \]

\(Y\)  Outcome variable
\(X\)  Explanatory variable
\(\beta\)  Slope (\(\frac{\text{rise}}{\text{run}}\))
\(\alpha\)  y-intercept

This is the smallest number of parameters to draw a line

We can think of intercept and slope as estimands

Conditional expectations

CEF \(E[Y|X]\) minimizes MSE of \(Y\) given \(X\)

If we restrict ourselves to a linear functional form \(Y = a + bX\)

then the following minimize MSE of \(Y\) given \(X\):

  • \(g(X) = \alpha + \beta X\) where
  • \(\alpha = E[Y] - \frac{\text{Cov}[X,Y]}{V[X]}E[X]\)
  • \(\beta = \frac{\text{Cov}[X,Y]}{V[X]}\)

So it’s really all about \(\beta\)

Aside: Regression and correlation

Informally, we use regression coefficients (slopes) to determine whether two variables are correlated

Technically, they are related but on a different scale

Regression coefficient: \(\beta = \frac{\text{Cov}[X,Y]}{V[X]}\)

Correlation: \(\rho = \frac{\text{Cov}[X,Y]}{SD[X] SD[Y]}\)

Aside: Regression and correlation

Informally, we use regression coefficients (slopes) to determine whether two variables are correlated

Technically, they are related but on a different scale

Regression coefficient: \(\beta = \frac{\text{Cov}[X,Y]}{V[X]}\) \(\Rightarrow\) in units of Y (happiness)

(Pearson’s) correlation: \(\rho = \frac{\text{Cov}[X,Y]}{SD[X] SD[Y]}\)

Aside: Regression and correlation

Informally, we use regression coefficients (slopes) to determine whether two variables are correlated

Technically, they are related but on a different scale

Regression coefficient: \(\beta = \frac{\text{Cov}[X,Y]}{V[X]}\) \(\Rightarrow\) in units of Y (happiness)

(Pearson’s) correlation: \(\rho = \frac{\text{Cov}[X,Y]}{SD[X] SD[Y]}\) \(\Rightarrow\) [-1, 1] scale

What are we doing?

  • Before: Assume there is a true parameter that we do not observe (e.g. population mean, ATE)

  • Now: Assume there is a true line that best describes the relationship between X and Y

  • There is a best linear predictor that we want to estimate

But how do we find it!?

Which line is a better summary?

More formally

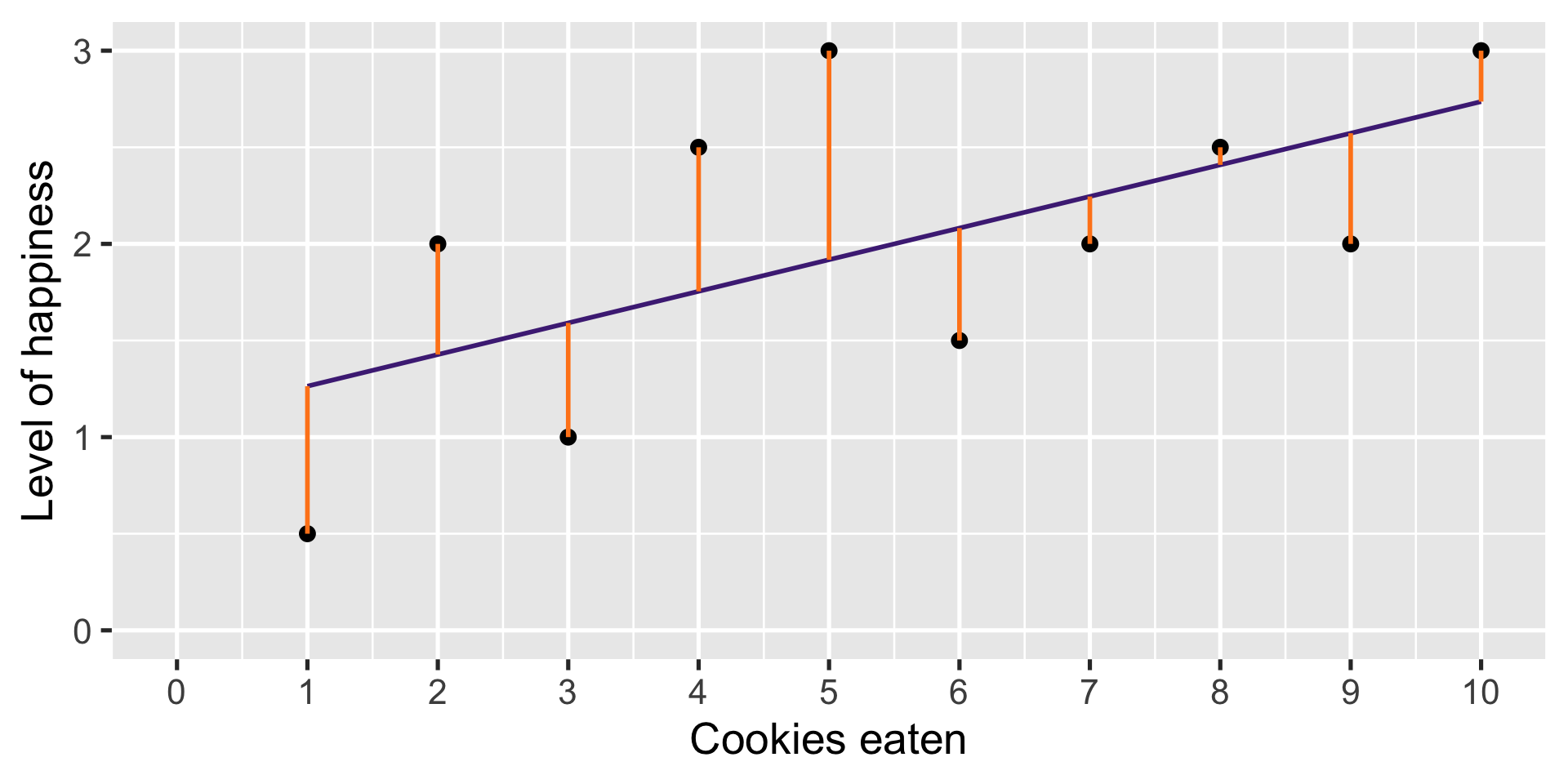
  • The best linear predictor is the line that minimizes the distance of each observation to the line

  • That distance is known as residual or error

Visualizing residuals

cookies_base +
  geom_smooth(method = "lm", color = nu_purple, se = FALSE)

Visualizing residuals

cookies_with_residual <- cookies_base +
  geom_smooth(method = "lm", color = nu_purple, se = FALSE) +
  geom_segment(aes(xend = cookies, yend = .fitted), color = "#FF851B", size = 1)

cookies_with_residual

More formally

  • The best linear predictor is the line that minimizes the distance of each observation to to the line

  • That distance is know as a residual or error

\[ e_i = (y_i - \widehat y_i) \]

More formally

  • The best linear predictor is the line that minimizes the distance of each observation to to the line

  • That distance is know as a residual or error

\[ e_i = (y_i - (b_0 + b_1 x_{1i})) \]

Minimizing residuals

We want to find a vector of coefficients (\(\widehat \beta_0\), \(\widehat \beta_1\)) that minimizes the sum of squared residuals

\[ SSR = \sum_{i=1}^n e_i^2 \]

We could try many lines until we find the the smallest SSR

Or use a method called Ordinary Least Squares (OLS)

OLS regression by plug-in principle

Estimand

\(\alpha = E[Y] - \frac{\text{Cov}[X,Y]}{V[X]}E[X] \qquad \beta = \frac{\text{Cov}[X,Y]}{V[X]}\)

 

Estimator

\(\widehat\alpha = \overline Y - \frac{\overline{XY} - \overline{X} \cdot \overline{Y}}{\overline{X^2} - \overline{X}^2} \overline{X} \qquad \widehat{\beta} = \frac{\overline{XY} - \overline{X} \cdot \overline{Y}}{\overline{X^2} - \overline{X}^2}\)

Back to cookies

\[ \widehat{y} = \widehat \beta_0 + \widehat \beta_1 x_1 \]

Back to cookies

\[ \widehat{\text{happiness}} = \beta_0 + \beta _1 \text{cookies} \]

Back to cookies

\(\widehat{\text{happiness}} = \beta_0 + \beta_1 \text{cookies}\)

Back to cookies

\(\widehat{\text{happiness}} = \beta_0 + \beta_1 \text{cookies}\)

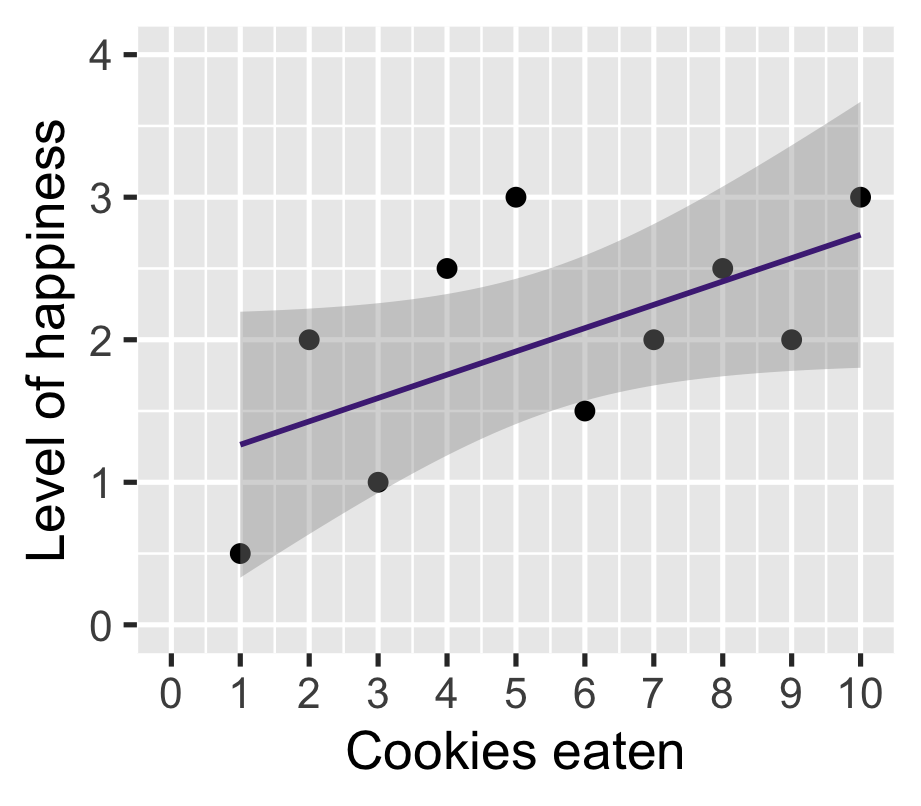
Back to cookies

\(\widehat{\text{happiness}} = \beta_0 + \beta_1 \text{cookies}\)

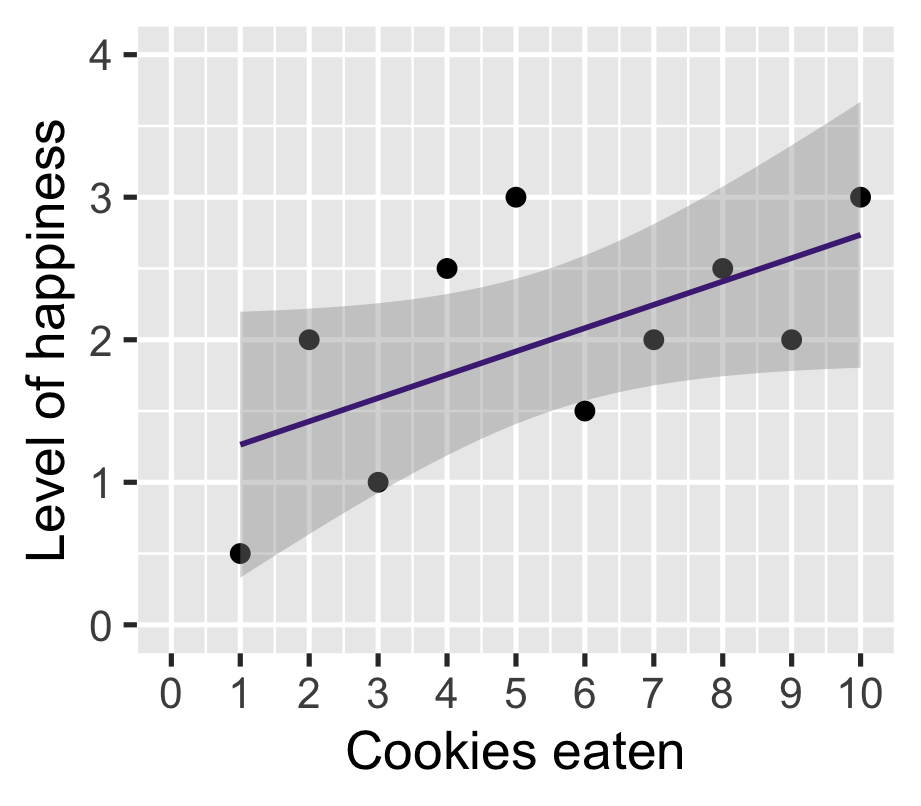
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164+
(0.076)
Num.Obs. 10
R2 0.368
+ p < 0.1, * p < 0.05, ** p < 0.01, *** p < 0.001

Back to cookies

\(\widehat{\text{happiness}} = \beta_0 + \beta_1 \text{cookies}\)

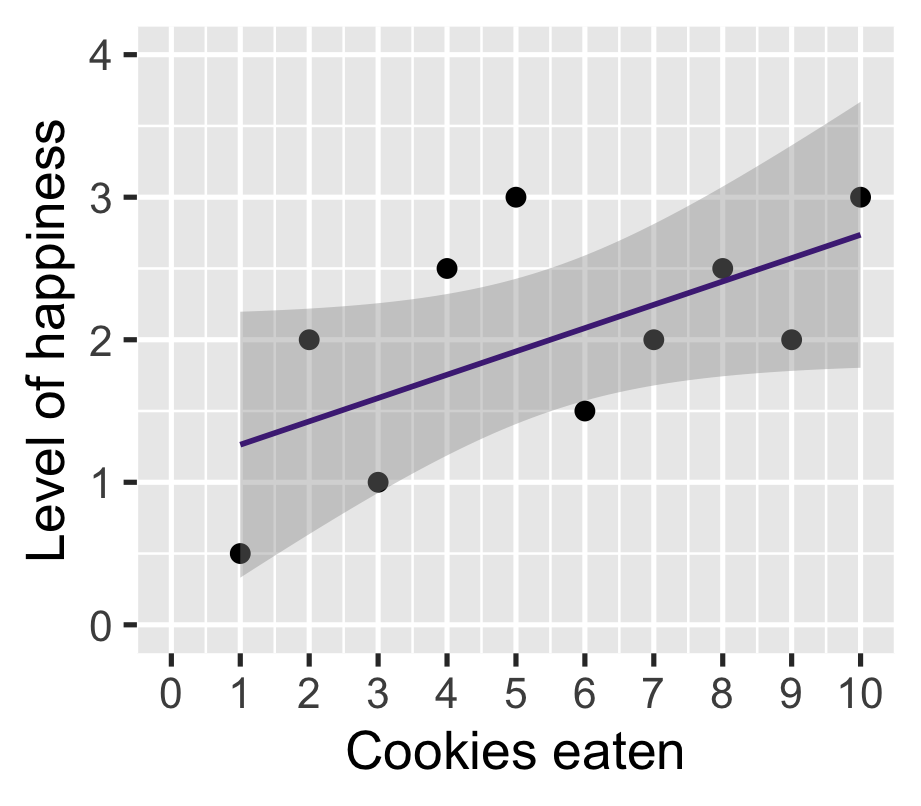
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

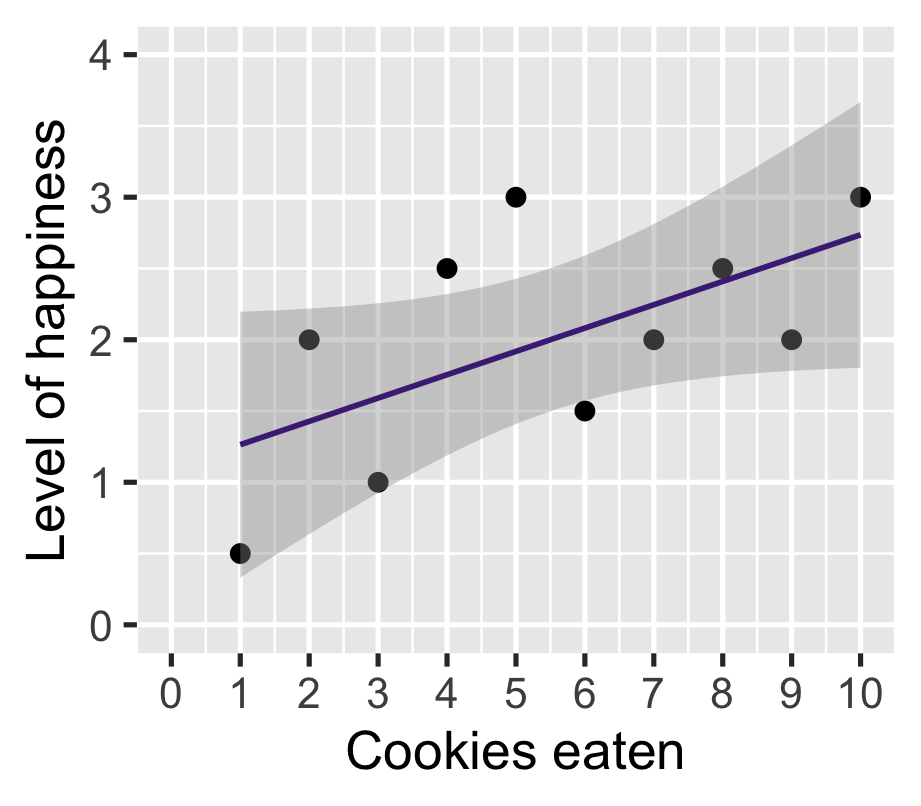
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

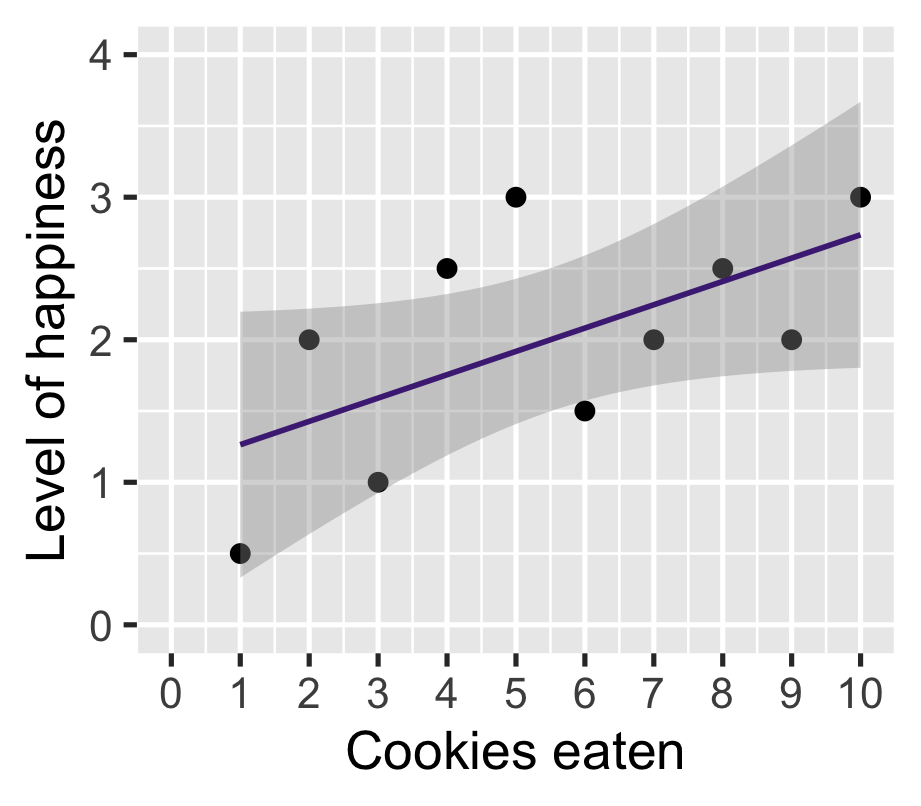
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

On average

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

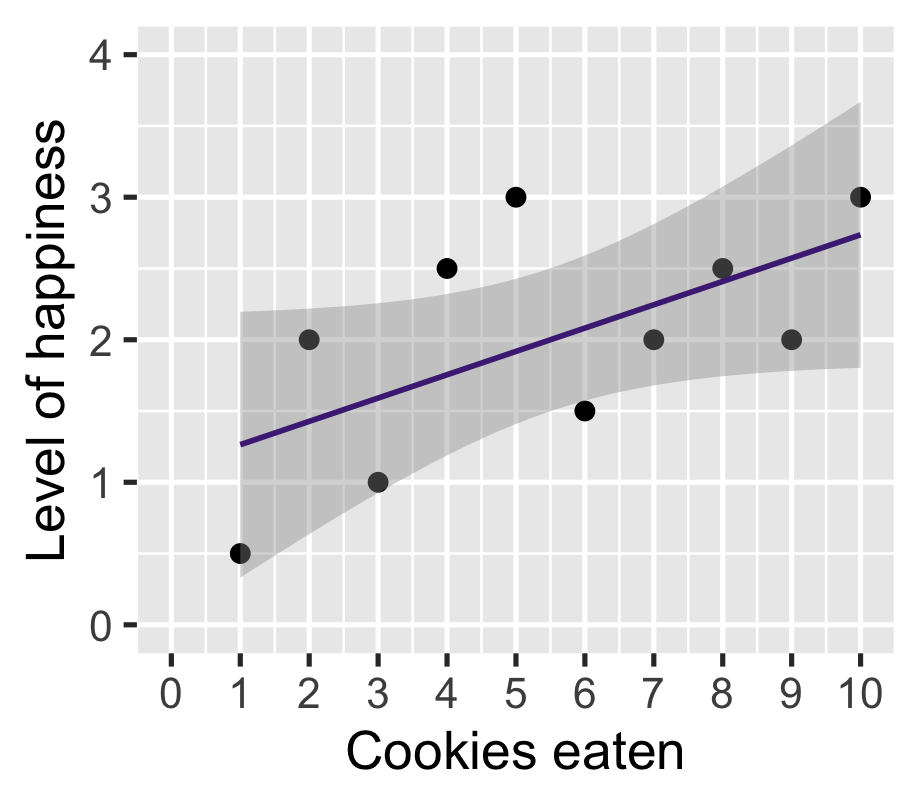
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

On average, one additional cookie

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

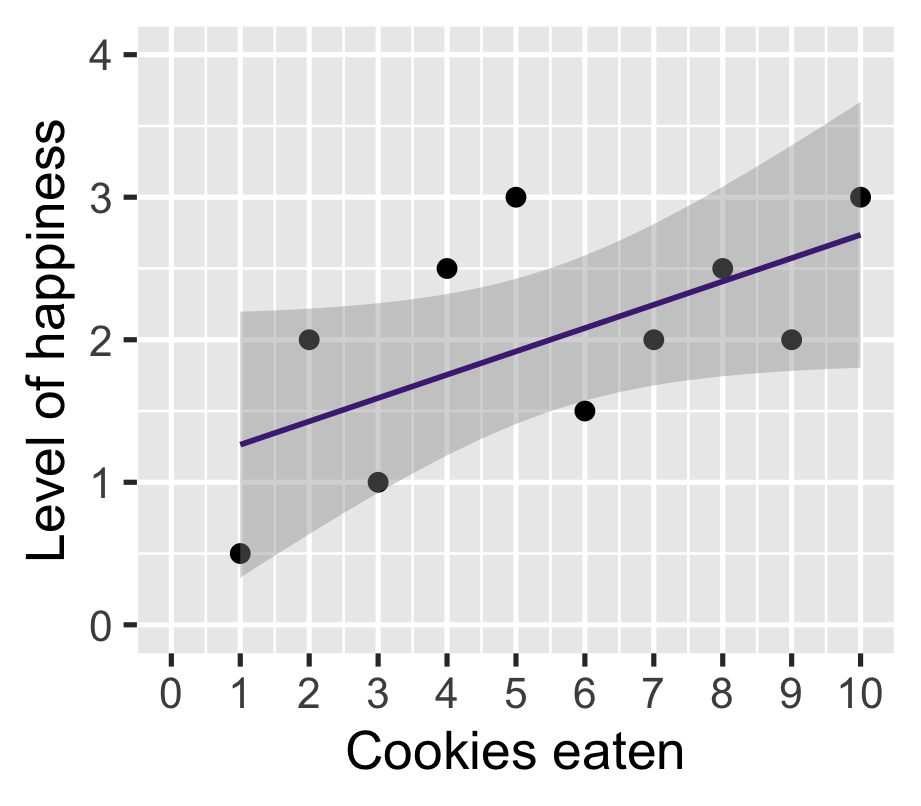
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

On average, one additional cookie increases happiness by 0.16 points

Helpful for comparison

Is 0.16 happiness points per cookie a lot?

We cannot tell without a point of reference

But correlation is a reference on its own:

Absolute magnitude Effect
0.1 Small
0.3 Moderate
0.5 Large

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

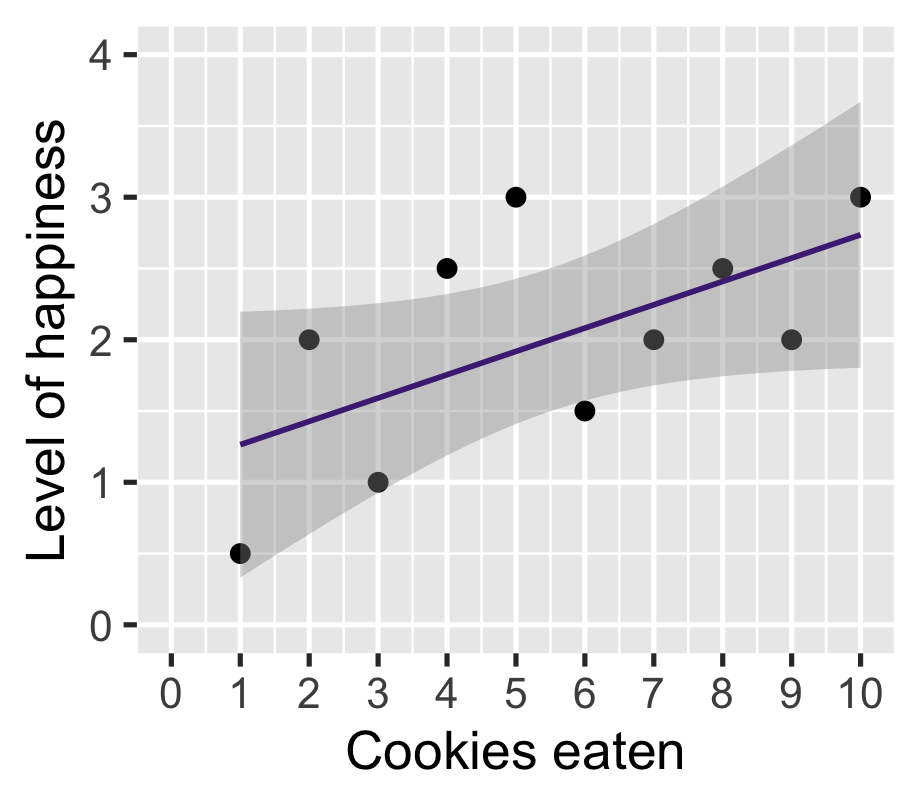
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

On average, one additional cookie increases happiness by 0.16 points

Back to cookies

\(\widehat{\text{happiness}} = 1.10 + 0.16 \cdot \text{cookies}\)

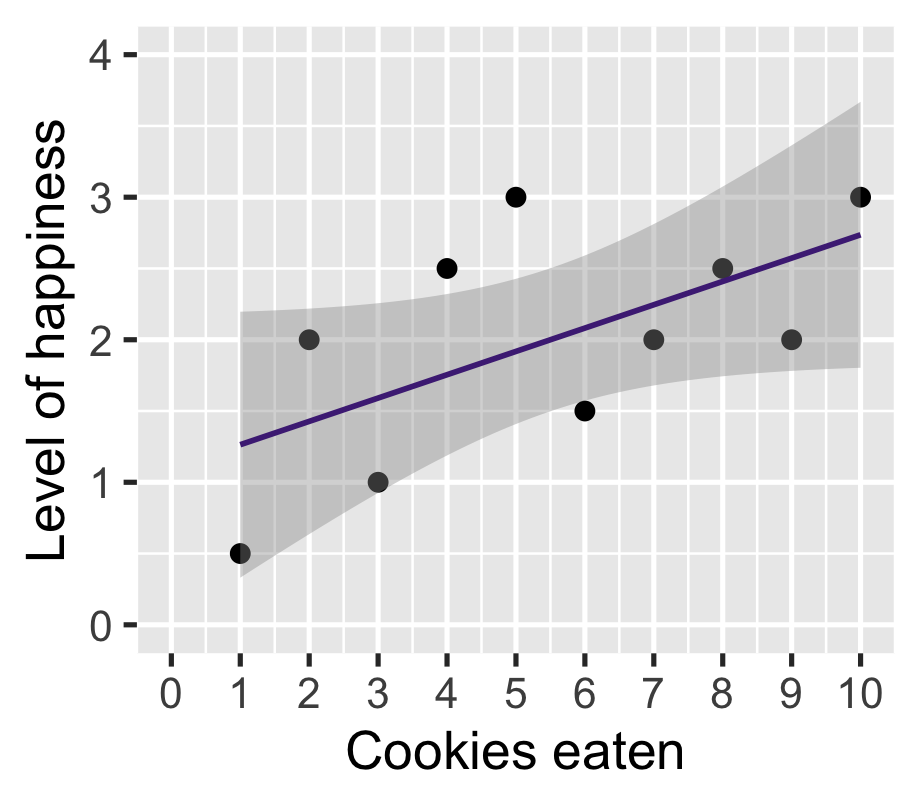
happinness
(Intercept) 1.100*
(0.470)
cookies 0.164
(0.076)
Num.Obs. 10
R2 0.368
* p < 0.05

On average, one additional cookie increases happiness by 0.16 points

Corresponds to \(\rho =\) 0.61

Multivariate regression

Problem

What if we wanted to include more variables?

Of course we can!

But why would we want do that?

Depends on what you want to say

  • Level 1: Description of conditional means

  • Level 2: Statistical inference (needs CIs or p-values)

  • Level 3: Causal inference (needs assumptions)

My take: You only care about level 2 because you have (at least) a proto-causal story

Meaning there is a focal X and Y relationship we want to measure, but it is “contaminated” by some confounder

We need to “adjust” or “control” the effect of X on Y (more in 3 weeks)

Ordinary Least Squares (OLS)

Rewrite with an arbitrary number of variables

Function \(\widehat{g} = \widehat \beta_0 + \widehat \beta_1 X_{[1]} + \widehat \beta_2 X_{[2]} + \ldots + \widehat \beta_K X_{[K]}\)

Such that

\[ \mathbf{\widehat \beta} = (\widehat\beta_0, \widehat\beta_1, \ldots, \widehat\beta_K) = \underset{(b_0, b_1, \ldots, b_K) \in \mathbb{R}^{K + 1}}{\text{argmin}} \frac{1}{n} \sum_{i = 1}^n e_i^2 \]

Where \(e_i = (Y_i - (b_0 + b_1 X_{[1]i} + b_2 X_{[2]i} + \ldots + b_K X_{[K]i}))\)

Ordinary Least Squares (OLS)

Rewrite with an arbitrary number of variables

Function \(\widehat{g} = \widehat \beta_0 + \widehat \beta_1 X_{[1]} + \widehat \beta_2 X_{[2]} + \ldots + \widehat \beta_K X_{[K]}\)

Such that

\[ \mathbf{\widehat \beta} = (\widehat\beta_0, \widehat\beta_1, \ldots, \widehat\beta_K) = \underset{(b_0, b_1, \ldots, b_K) \in \mathbb{R}^{K + 1}}{\text{argmin}} \frac{1}{n} \sum_{i = 1}^n e_i^2 \]

Where \(e_i = (Y_i - \widehat Y_i)\)

Ordinary Least Squares (OLS)

Rewrite with an arbitrary number of variables

Function \(\widehat{g} = \widehat \beta_0 + \widehat \beta_1 X_{[1]} + \widehat \beta_2 X_{[2]} + \ldots + \widehat \beta_K X_{[K]}\)

Such that

\[ \mathbf{\widehat \beta} = (\widehat\beta_0, \widehat\beta_1, \ldots, \widehat\beta_K) = \underset{(b_0, b_1, \ldots, b_K) \in \mathbb{R}^{K + 1}}{\text{argmin}} \frac{1}{n} \sum_{i = 1}^n e_i^2 \]

Where \(e_i = (\text{actual} - \text{predicted})\)

ANES 2016 data

# remotes::install_github("jamesmartherus/anesr")
library(anesr)


data(timeseries_2016)

Variables

nes16 = timeseries_2016 %>% 
  select(
    V162079, # Feeling thermometer for TRUMP [POST]
    V162230x, # Better if man works and woman takes care of home [POST]
    V162255, # Is Barack Obama Muslim (yes/no) [POST]
    V161267, # Respondent Age [PRE]
    V161270, # Highest level of Education (Years) [PRE]
    V161158x # Party ID [PRE]
  )
# A tibble: 4,270 × 6
   V162079    V162230x   V162255    V161267    V161270    V161158x  
   <hvn_lbll> <hvn_lbll> <hvn_lbll> <hvn_lbll> <hvn_lbll> <hvn_lbll>
 1 85         4           2         29          9         7         
 2 60         4           1         26         13         6         
 3 70         1           1         23          9         3         
 4 60         1           2         58          9         5         
 5 15         4           1         38          9         3         
 6 65         4          -8         60         14         5         
 7 50         4          -8         58          5         1         
 8 85         1           1         56          9         4         
 9 70         4           2         45          9         5         
10 60         4          -8         30         10         3         
# ℹ 4,260 more rows

Recode

nes16 = nes16 %>% 
  mutate(
    ft_trump_post = ifelse(V162079 < 0 | V162079 == 998, NA, V162079),
    women_at_home = case_when(V162230x < 0 ~ NA,
                              V162230x <= 3 ~ 1,
                              V162230x <= 7 ~ 0),
    obamamuslim = ifelse(V162255 == 1, 1, 0),
    age = ifelse(V161267 < 0, NA, V161267),
    age0 = age - 18,
    educ_hs = case_when(V161270 < 0 ~ NA,
                        V161270 >= 90 ~ NA,
                        V161270 >= 9 ~ 1,
                        V161270 <= 8 ~ 0),
    republican = case_when(V161158x < 0 ~ NA,
                           V161158x <= 4 ~ 0,
                           V161158x <= 7 ~ 1)
  )
nes = nes16 %>% 
  select(ft_trump_post,
         women_at_home, obamamuslim,
         age, age0,
         educ_hs, republican)
# A tibble: 4,270 × 7
   ft_trump_post women_at_home obamamuslim   age  age0 educ_hs republican
           <dbl>         <dbl>       <dbl> <dbl> <dbl>   <dbl>      <dbl>
 1            85             0           0    29    11       1          1
 2            60             0           1    26     8       1          1
 3            70             1           1    23     5       1          0
 4            60             1           0    58    40       1          1
 5            15             0           1    38    20       1          0
 6            65             0           0    60    42       1          1
 7            50             0           0    58    40       0          0
 8            85             1           1    56    38       1          0
 9            70             0           0    45    27       1          1
10            60             0           0    30    12       1          0
# ℹ 4,260 more rows

Main relationship

ggplot(nes) +
  aes(x = obamamuslim,
      y = ft_trump_post) +
  geom_jitter(size = 1, 
              width = 0.3,
              alpha = 0.8,
              color = nu_purple) +
  scale_x_continuous(breaks = c(0, 1))

Regression as conditional means

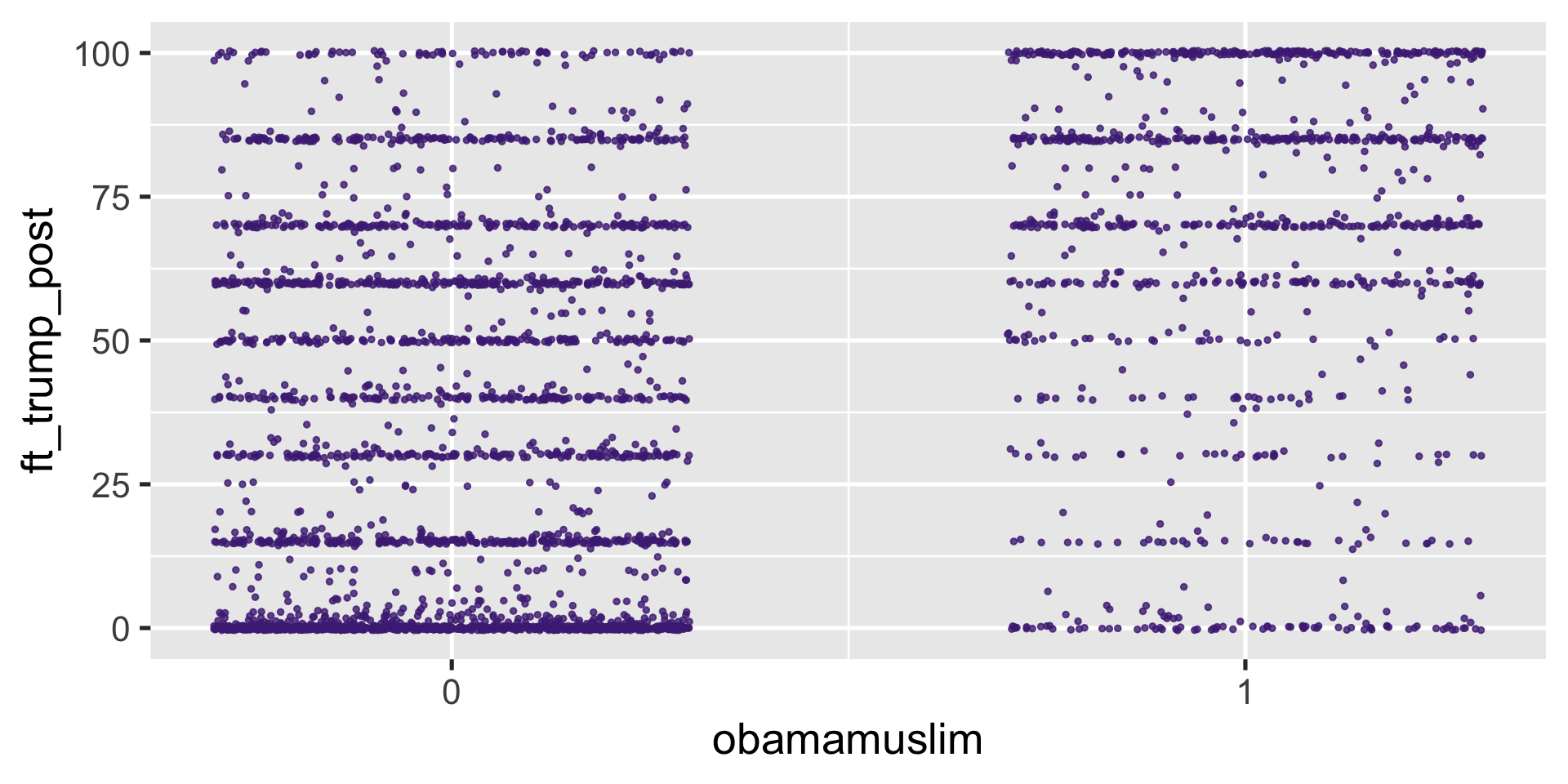
\(\widehat{\texttt{ft_trump_post}} = \beta_0 + \beta_1 \cdot \texttt{obamamuslim}\)

lm_race = lm(ft_trump_post ~ obamamuslim, data = nes)
term estimate std.error p.value
(Intercept) 32.17 0.61 0
obamamuslim 35.04 1.15 0

Regression as conditional means

\(\widehat{\texttt{ft_trump_post}} = 32.17 + 35.04 \cdot \texttt{obamamuslim}\)

lm_race = lm(ft_trump_post ~ obamamuslim, data = nes)
term estimate std.error p.value
(Intercept) 32.17 0.61 0
obamamuslim 35.04 1.15 0

  • What is the average feeling thermometer for someone who does not believe Obama is a Muslim?

  • What is the average feeling thermometer for someone who does believe Obama is a Muslim?

Regression as conditional means

Compare with

nes %>% 
  select(ft_trump_post, obamamuslim) %>% 
  drop_na() %>% 
  group_by(obamamuslim) %>% 
  summarize(estimate = mean(ft_trump_post))
# A tibble: 2 × 2
  obamamuslim estimate
        <dbl>    <dbl>
1           0     32.2
2           1     67.2
sum(coef(lm_race))
[1] 67.20505

Maybe just an education thing

coef(lm(obamamuslim ~ educ_hs, data = nes))
(Intercept)     educ_hs 
 0.28368794 -0.04484413 
coef(lm(ft_trump_post ~ educ_hs, data = nes))
(Intercept)     educ_hs 
  44.991228   -3.083431 
with(nes, cor(educ_hs, obamamuslim, use = "pairwise.complete.obs"))
[1] -0.02613526
Absolute magnitude Effect
0.1 Small
0.3 Moderate
0.5 Large

Or maybe an age thing

coef(lm(obamamuslim ~ age, data = nes))
(Intercept)         age 
0.176466090 0.001301993 
summary(nes$age)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
  18.00   34.00   50.00   49.58   63.00   90.00     121 
summary(nes$age0)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
   0.00   16.00   32.00   31.58   45.00   72.00     121 
coef(lm(obamamuslim ~ age0, data = nes))
(Intercept)        age0 
0.199901973 0.001301993

Or maybe an age thing

coef(lm(ft_trump_post ~ age0, data = nes))
(Intercept)        age0 
 34.3998310   0.2424554 
with(nes, cor(age, obamamuslim, use = "pairwise.complete.obs"))
[1] 0.05350295

Or partisan motivated reasoning

coef(lm(obamamuslim ~ republican, data = nes))
(Intercept)  republican 
  0.1445592   0.2388995 
coef(lm(ft_trump_post ~ republican, data = nes))
(Intercept)  republican 
   24.21449    43.88579 
with(nes, cor(republican, obamamuslim, use = "pairwise.complete.obs"))
[1] 0.2741116

Adjusting for covariates

coef(lm(ft_trump_post ~ obamamuslim, data = nes))
(Intercept) obamamuslim 
   32.16788    35.03717 
coef(lm(ft_trump_post ~ obamamuslim + educ_hs, data = nes))
(Intercept) obamamuslim     educ_hs 
 32.7625038  34.8518643  -0.5570192 
coef(lm(ft_trump_post ~ obamamuslim + educ_hs + age0, data = nes))
 (Intercept)  obamamuslim      educ_hs         age0 
26.557225629 34.563705332  0.006911287  0.183081786 
coef(lm(ft_trump_post ~ obamamuslim + educ_hs + age0 + republican,
        data = nes))
(Intercept) obamamuslim     educ_hs        age0  republican 
 23.1524906  22.2249306  -6.2160330   0.1007929  37.5392727

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

Side by side

(1) (2) (3) (4) (5)
(Intercept) 32.168* 32.763* 23.090* 20.367* 21.338*
(0.611) (2.104) (1.574) (0.581) (2.157)
obamamuslim 35.037* 34.852* 34.715* 22.742* 22.225*
(1.147) (1.154) (1.162) (0.996) (1.016)
educ_hs -0.557 -6.216*
(2.135) (1.788)
age 0.185* 0.101*
(0.030) (0.025)
republican 37.533* 37.539*
(0.913) (0.933)
Num.Obs. 3632 3601 3536 3616 3496
R2 0.204 0.203 0.214 0.459 0.462
* p < 0.05

We are (presumably) reducing bias, but increasing variance (standard errors)

Visualizing

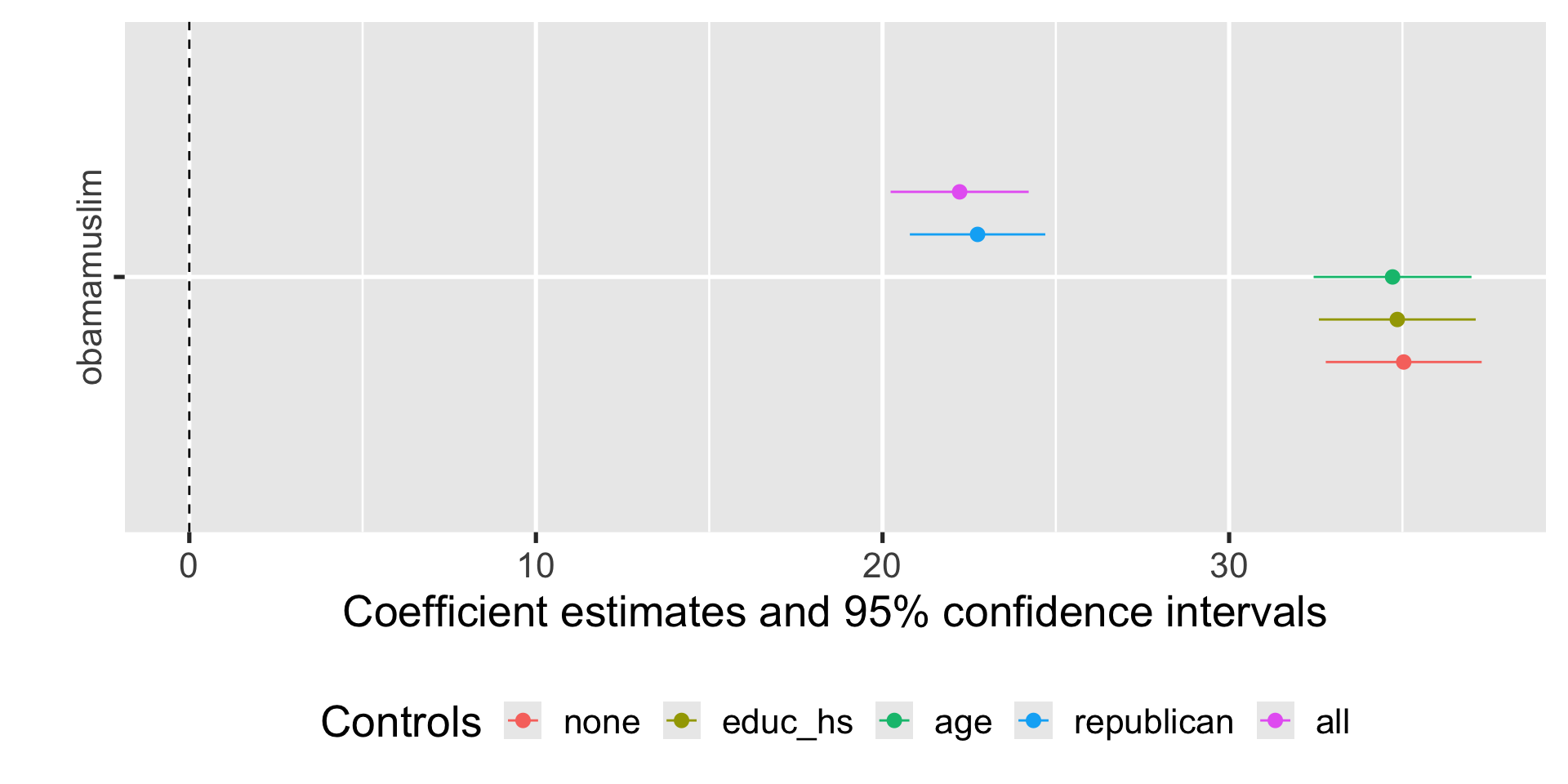
Everything else constant

Plug-in coefficients in equations:

\(\widehat{\texttt{ft_trump_post}} = 32.17 + 35.04 \cdot \texttt{obamamuslim}\)

\(\widehat{\texttt{ft_trump_post}} = 32.76 + 34.85 \cdot \texttt{obamamuslim} -0.56 \cdot \texttt{educ_hs}\)

\(\widehat{\texttt{ft_trump_post}} = 23.09 + 34.72 \cdot \texttt{obamamuslim} + 0.19 \cdot \texttt{age}\)

\(\widehat{\texttt{ft_trump_post}} = 20.367 + 22.74 \cdot \texttt{obamamuslim} + 37.53 \cdot \texttt{republican}\)

\(\widehat{\texttt{ft_trump_post}} = 21.34 + 22.23 \cdot \texttt{obamamuslim} -6.22 \cdot \texttt{educ_hs} +\\ 0.10 \cdot \texttt{age} + 37.54 \cdot \texttt{republican}\)

 

Coefficients now need to be interpreted as marginal means or marginal slopes

 

These only make sense if you think at least one variable is a focal point

Heterogeneous effects

What if we believed the effect of obamamuslim varies depending on attitudes about gender roles?

Interactions

Code

Math

coef(lm(ft_trump_post ~ women_at_home,
        data = nes))
  (Intercept) women_at_home 
     35.84525      17.58167

\(y = \beta_0 + \beta_1 \mathtt{\text{women_at_home}} + \varepsilon\)

coef(lm(ft_trump_post ~ 
          obamamuslim + women_at_home,
        data = nes))
  (Intercept)   obamamuslim women_at_home 
     28.21032      32.92204      12.66395

\(y = \beta_0 + \beta_1 \mathtt{obamamuslim} + \beta_2 \mathtt{\text{women_at_home}} + \varepsilon\)

coef(lm(ft_trump_post ~ 
          obamamuslim * women_at_home,
        data = nes)) %>% 
  tidy() # easier to read in slides
# A tibble: 4 × 2
  names                         x
  <chr>                     <dbl>
1 (Intercept)               27.7 
2 obamamuslim               34.9 
3 women_at_home             14.2 
4 obamamuslim:women_at_home -4.74

\[ \begin{align*} y = & \beta_0 + \beta_1 \mathtt{obamamuslim} + \beta_2 \mathtt{\text{women_at_home}} + \\ & \beta_3 \mathtt{obamamuslim} \times \mathtt{\text{women_at_home}} + \varepsilon \end{align*} \]

Caution

The linear model setup is flexible

\[\widehat{y} = \widehat \beta_0 + \widehat \beta_1 x_1 + \widehat \beta_2 x_2 + \ldots + \widehat \beta_K x_K\]

You can technically put whatever you want in a regression as long as \(\text{observations} > \text{variables}\)

But for statistical or causal inference, anything with more than 2-3 control variables doesn’t make much sense

Increasing dimensions

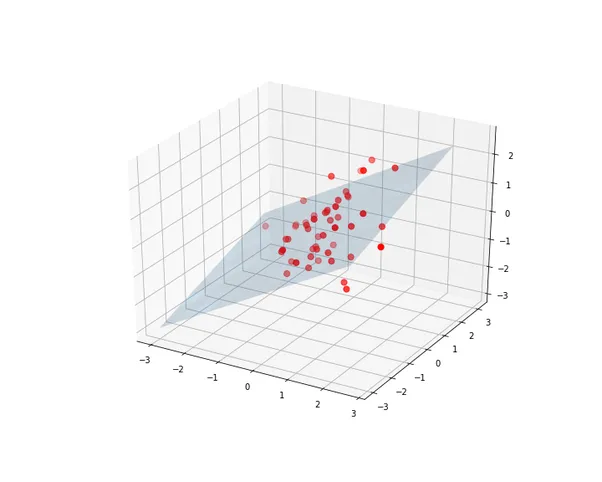
Increasing dimensions

More dimensions \(\rightarrow\) more likely to see:

  • Extrapolation: Fitting line beyond actual range

  • Interpolation: Gaps within actual range

Illusion of learning from empty space!

AM call this overfitting

Wrapping up

Wrapping up

  • Regression as the go-to method to estimate conditional means

  • Best Linear Unbiased Estimator (BLUE)

  • Multivariate regression only makes sense with a marginal means interpretation

  • Which requires a (proto-)causal story

  • And stops making sense with too many controls

Fun: OLS with matrix algebra

Outcome: \(n \times 1\) column vector

\[Y = \begin{bmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_n \end{bmatrix}\]

Fun: OLS with matrix algebra

Explanatory variables: \(n \times (k+1)\) matrix

\[X= \begin{bmatrix} 1 & x_{11} & \dots & x_{1k} \\ 1 & x_{21} & \dots & x_{2k} \\ \vdots & \vdots & \dots & \vdots \\ 1 & x_{n1} & \dots & x_{nk} \end{bmatrix}\]

\(x_{ij}\) is the \(i\)-th observation of the \(j\)-th explanatory variable.

Linear regression model

Let’s say we have 173 observations (n = 173) and 2 explanatory variables (k = 3)

Equation: \(y = \beta_0 + \beta_1x_1 + \beta_2x_2\)

Matrix form: \[\begin{aligned} \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix} = \begin{bmatrix} 1 & x_{11} & x_{21} \\ 1 & x_{21} & x_{22} \\ \vdots & \vdots & \vdots \\ 1 & x_{1173} & x_{2173} \end{bmatrix} \begin{bmatrix} \beta_0 \\ \beta_1 \\ \beta_2 \end{bmatrix}\end{aligned} \]

Estimation

\[\hat{\beta} = (X'X)^{-1}X'Y\]

“X prime X inverse, X prime Y”

Example

cars_df = mtcars
Y = as.matrix(cars_df$mpg)
      [,1]
 [1,] 21.0
 [2,] 21.0
 [3,] 22.8
 [4,] 21.4
 [5,] 18.7
 [6,] 18.1
 [7,] 14.3
 [8,] 24.4
 [9,] 22.8
[10,] 19.2
[11,] 17.8
[12,] 16.4
[13,] 17.3
[14,] 15.2
[15,] 10.4
[16,] 10.4
[17,] 14.7
[18,] 32.4
[19,] 30.4
[20,] 33.9
[21,] 21.5
[22,] 15.5
[23,] 15.2
[24,] 13.3
[25,] 19.2
[26,] 27.3
[27,] 26.0
[28,] 30.4
[29,] 15.8
[30,] 19.7
[31,] 15.0
[32,] 21.4

Example

cars_df = mtcars
Y = as.matrix(cars_df$mpg)
# create two separate matrices for IVs
X1 = as.matrix(cars_df$hp)
X2 = as.matrix(cars_df$wt)

# bind them altogether into one matrix
# with constant column
constant =  rep(1, nrow(cars_df))
X = cbind(constant, X1, X2)
      constant          
 [1,]        1 110 2.620
 [2,]        1 110 2.875
 [3,]        1  93 2.320
 [4,]        1 110 3.215
 [5,]        1 175 3.440
 [6,]        1 105 3.460
 [7,]        1 245 3.570
 [8,]        1  62 3.190
 [9,]        1  95 3.150
[10,]        1 123 3.440
[11,]        1 123 3.440
[12,]        1 180 4.070
[13,]        1 180 3.730
[14,]        1 180 3.780
[15,]        1 205 5.250
[16,]        1 215 5.424
[17,]        1 230 5.345
[18,]        1  66 2.200
[19,]        1  52 1.615
[20,]        1  65 1.835
[21,]        1  97 2.465
[22,]        1 150 3.520
[23,]        1 150 3.435
[24,]        1 245 3.840
[25,]        1 175 3.845
[26,]        1  66 1.935
[27,]        1  91 2.140
[28,]        1 113 1.513
[29,]        1 264 3.170
[30,]        1 175 2.770
[31,]        1 335 3.570
[32,]        1 109 2.780

Calculate \(\hat{\beta} = (X'X)^{-1}X'Y\)

# X prime X
XpX = t(X) %*% X

# X prime X inverse
XpXinv = solve(XpX)

# X prime Y
XpY = t(X) %*% Y

# beta coefficient estimates
# X prime X inverse, X prime Y
bhat = XpXinv %*% XpY

Compare:

c(bhat)
[1] 37.22727012 -0.03177295 -3.87783074
lm(mpg ~ hp + wt, data = mtcars) %>% coef()
(Intercept)          hp          wt 
37.22727012 -0.03177295 -3.87783074