Parametric Models

POLI_SCI 403: Probability and Statistics

Agenda

• Main idea
• Parametric regression
• Binary choice models (logistic regression)
• Maximum likelihood estimation
• Lab

Parametric Models

So far

• Agnostic statistics approach: Assume only what can be gleaned from data

• No need to make distributional assumptions, only i.i.d. process

• Meaning our approach is non-parametric

• Alternative: Parametric models

What does “parametric” mean?

• Parametric: Assume full functional form with finite number of parameters

• Nonparametric: Assume functional form is unknown, possibly infinite number of parameters

• Semiparametric: ¯\(ツ)/¯

Ingredients of a parametric model

• Set of functions \(g\)
• Indexed by parameter vector \(\theta\)
• Model is true for every \(\theta\) if…
• \(f_{Y|X}(y|x) = g(y,x; \theta)\)

We assume there exists a function \(g\) with parameters \(\theta\)

If you know \(\theta\), then you can fully characterize the PMF/PDF of \(Y\) given \(X\)

Then we can say \(\theta\) is a sufficient statistic

Toy example: Biased coin flip

\[ f_Y(y) = g(y;p) = \begin{cases} 1-p &:& y = 0\\ p &:& y=1\\ 0 &:& \text{otherwise.} \end{cases} \]

• \(\theta = p\)
• If you know \(p\), then you fully know the distribution of random variable \(Y\)

Regression

again

Classical linear model

\[ Y = \boldsymbol{X \beta} + \varepsilon \]

• \(Y\): Response (Outcome)
• \(X\): Matrix of predictors (explanatory variables)
• \(\boldsymbol{\beta} = (\beta_0, \beta_1, \ldots, \beta_K)^T\) Vector of coefficients
• \(\varepsilon \sim N(0, \sigma^2)\) Errors (residuals) i.i.d. normal with expectation zero

If you know \(\boldsymbol{\beta}\) and \(\sigma^2\), then you can fully characterize the PMF/PDF of \(Y\) given \(X\)

Why do we need \(\varepsilon \sim N(0, \sigma^2)\)?

• \(\boldsymbol{\beta}\) represents the variation in \(Y\) that comes from predictors \(\boldsymbol{X}\)
• \(\varepsilon\) represents variation in \(Y\) that cannot be attributed to \(\boldsymbol{X}\)
• If errors are i.i.d. then they are also independent of \(\boldsymbol{X}\)
• We need this so that our estimator is unbiased by definition

\[ Y = \beta_0 + \beta_1 X_1 + \varepsilon \]

\[ Y = \beta_0 + \beta_1 X_1 + \color{purple}{\beta_2 X_2} + \varepsilon \]

Dr. Huntington-Klein explains it better

Binary Choice Models

Logistic regression

Parametric model

\[ g(y, \boldsymbol{X}; \beta) = \begin{cases} 1-h(\boldsymbol{X\beta}) &:& y = 0\\ h(\boldsymbol{X\beta}) &:& y = 1 \\ 0 &:& \text{otherwise.} \end{cases} \]

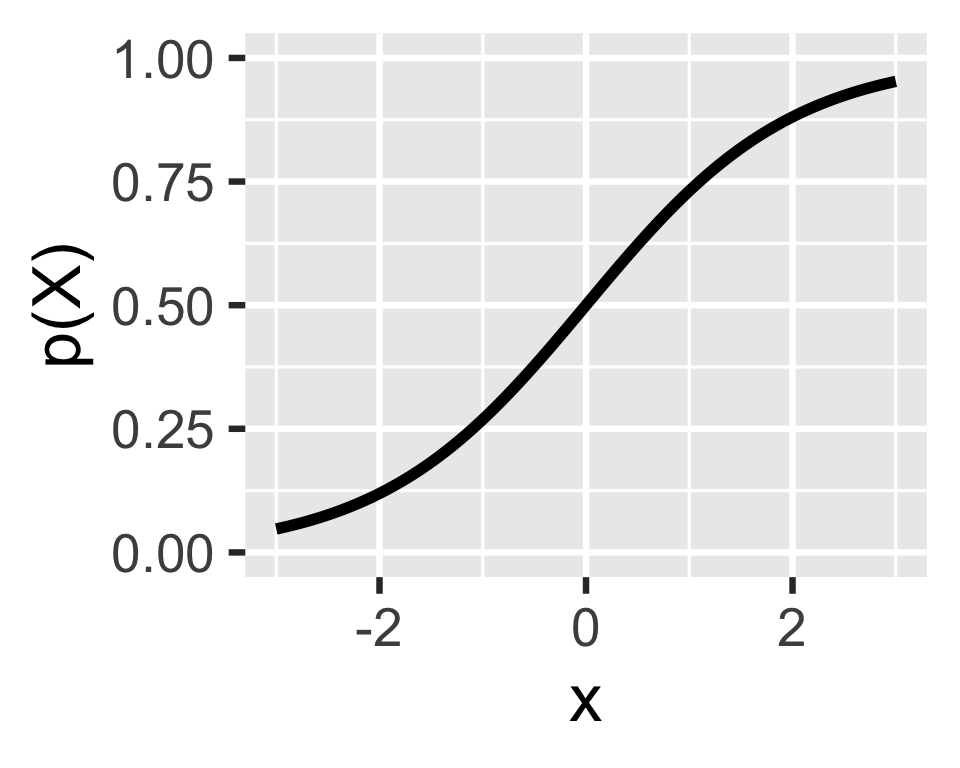
Let \(h(\boldsymbol{X\beta}) = Pr(Y = 1 | X) = p(X)\) for simplicity

Called logit model in the AM textbook

Logistic regression

Parametric model

\[ g(y, \boldsymbol{X}; \beta) = \begin{cases} 1-h(\boldsymbol{X\beta}) &:& y = 0\\ h(\boldsymbol{X\beta}) &:& y = 1 \\ 0 &:& \text{otherwise.} \end{cases} \]

Called logit model in the AM textbook

Logistic regression

Parametric model

\[ g(y, \boldsymbol{X}; \beta) = \begin{cases} 1-p(X) &:& y = 0\\ p(X) &:& y = 1 \\ 0 &:& \text{otherwise.} \end{cases} \]

• \(\boldsymbol{\beta} = (\beta_0, \beta_1, \ldots, \beta_K)^T\)
• \(p(X)\) or \(h(\boldsymbol{X\beta})\) is the mean or link function
• We need the link to bound \(y\) in the \([0,1]\) range

Called logit model in the AM textbook

Logistic regression

For the logit model, the link is the logistic function

\[ p(X) = \frac{e^{X\beta}}{1+e^{X\beta}} \]

Logistic regression

For the logit model, the link is the logistic function

\[ p(X) = \frac{e^{X\beta}}{1+e^{X\beta}} \]

Rearrange to get the odds ratio

\[ \frac{p(X)}{1-p(X)} = e^{{X\beta}} \]

This is still a linear model in the sense that it is linear in parameters

Logistic regression

Taking the natural logarithm gives the log odds

\[ log \left (\frac{p(X)}{1-p(X)} \right) = X\beta \]

• Weird to interpret, easy to estimate
• It’s called logit because you need to log it to make it easier to estimate
• How do we estimate?

Notice we are not making assumptions about an error term because we are modeling a Bernoulli distribution

Maximum likelihood estimation (MLE)

• Knowing \(\theta\) is enough to characterize conditional PMF of \(Y\) given \(X\)
• But we do not know \(\theta\)! We only know the data we observe
• We can try many different values for \(\theta\) and see what sticks
• Trick: Find \(\theta\) that would have maximized the probability of obtaining the data we observe
• Restated: Find parameters that would have made outcomes as likely as possible

Dr. King explains it better

Example: Which line makes observed data more likely?

More formally

Likelihood function \(\mathcal{L}(t|Y, \boldsymbol{X})\)

Maximum likelihood estimator

\[ \widehat{\theta}_{ML} = \underset{t\in\Theta}{\text{argmax}}\mathcal{L}(t|Y, \boldsymbol{X}) = \underset{t\in\Theta}{\text{argmax}} \prod_{i=1}^n\mathcal{L}(t|Y_i, \boldsymbol{X_i}) \]

Products are hard, maximize log-likelihood instead

\[ \widehat{\theta}_{ML} = \underset{t\in\Theta}{\text{argmax}}[\text{log}\mathcal{L}(t|Y, \boldsymbol{X})] = \underset{t\in\Theta}{\text{argmax}} \sum_{i=1}^n\text{log}\mathcal{L}(t|Y_i, \boldsymbol{X_i}) \]

Another way to look at it

How do you find the maximum likehihood?

Analytically

• Take the derivative of \(\text{log}\mathcal{L}(\theta|Y, X)\) w.r.t. \(\theta\)

• Set to \(0\), solve for \(\theta\) and label it \(\widehat \theta\) (if possible)

• Check if second derivative is negative (so it is maximum not minimum)

How do you find the maximum likehihood?

Numerically

Computer will do it for you

Use optimization algorithm to find maxima (if any)

Computationally intensive to write on your own

Most MLE methods have fast pre-packaged functions

Rule of thumb: If the algorithm takes too long, don’t believe the result!

With data

library(ISLR)

head(Default)

  default student   balance    income
1      No      No  729.5265 44361.625
2      No     Yes  817.1804 12106.135
3      No      No 1073.5492 31767.139
4      No      No  529.2506 35704.494
5      No      No  785.6559 38463.496
6      No     Yes  919.5885  7491.559

Default$default01 = ifelse(Default$default == "Yes", 1, 0)

with(Default, table(default, default01))

       default01
default    0    1
    No  9667    0
    Yes    0  333

Estimation

Linear probability model

ols = lm(default01 ~ student + balance + income, data = Default)

coef(ols) # very small numbers

  (Intercept)    studentYes       balance        income 
-8.117949e-02 -1.033010e-02  1.326897e-04  1.991528e-07 

Estimation

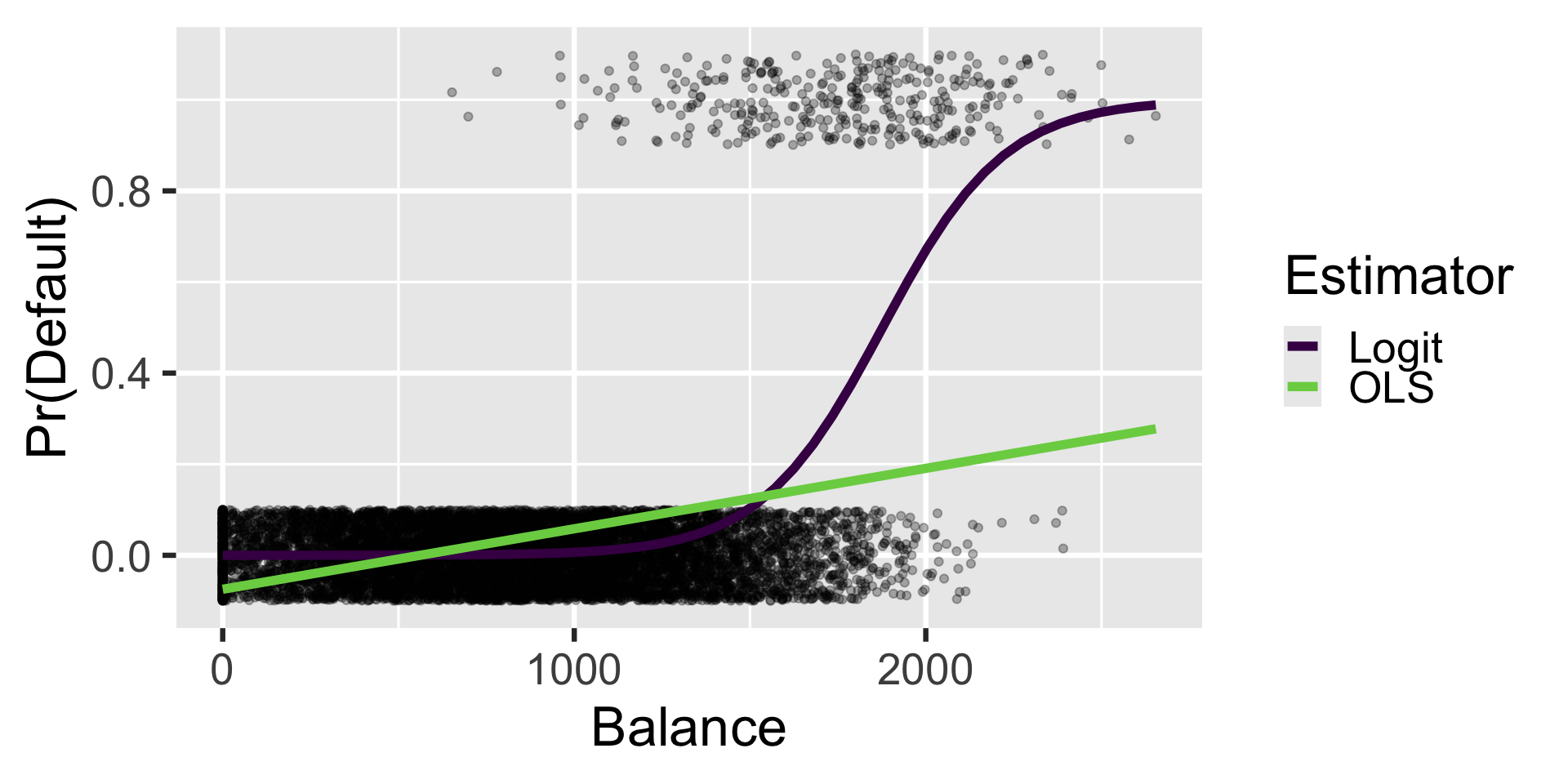
Linear probability model

ols = lm(default01 ~ student + balance + income, data = Default)

coef(ols) %>% round(5) # easier to read

(Intercept)  studentYes     balance      income 
   -0.08118    -0.01033     0.00013     0.00000 

Logit model

logit = glm(default01 ~ student + balance + income, 
            data = Default, family = binomial)

coef(logit) %>% round(5)

(Intercept)  studentYes     balance      income 
  -10.86905    -0.64678     0.00574     0.00000 

Logit coefficients are expressed in log-odds

Convert to probabilities

get_logit_prob = function(fit){
  coefs = coef(fit) # extract coefficients from logit fit
  odds = exp(coefs) # transform log-odds to odds
  prob = odds / (1 + odds) # convert odds to probabilities
  prob = round(prob, 5) # round for easy interpretation
  return(prob)
}

get_logit_prob(logit)

(Intercept)  studentYes     balance      income 
    0.00002     0.34372     0.50143     0.50000 

coef(ols) %>% round(5)

(Intercept)  studentYes     balance      income 
   -0.08118    -0.01033     0.00013     0.00000 

Why so different?

• Plot
• Code

library(marginaleffects)

# Extract predictions
p_ols = plot_predictions(ols,
                 condition = "balance",
                 draw = FALSE)

p_log = plot_predictions(logit,
                         condition = "balance",
                         draw = FALSE)

# Combine and label
pred_df = bind_rows(
  p_ols %>% mutate(Estimator = "OLS"),
  p_log %>% mutate(Estimator = "Logit")
)

# Visualize
ggplot(Default) +
  aes(x = balance, y = default01) +
  geom_jitter(alpha = 0.3, height = 0.1) +
  geom_line(
    data = pred_df,
    aes(x = balance, 
        y = estimate,
        color = Estimator),
    linewidth = 2) +
  scale_color_viridis_d(begin = 0, end = 0.8) +
  labs(x = "Balance",
       y = "Pr(Default)")

Why would you want to do this?

Critique: You can reverse engineer MLE so that your preferred parameters are optimal

Achen (2002, ARPS): Stop making up new parametric models!

Or, rather, motivate your parametric models with well-laid out formal model

So you get as close as possible to the microfoundations

Microfoundations: Explaining macro-level phenomena by modeling the behavior of individual agents

MLE finite sample properties

We said OLS was BLUE

MLE find the MVUE instead

MLE finite sample properties

1. Minimum

MLE finite sample properties

1. Minimum Variance

MLE finite sample properties

1. Minimum Variance Unbiased

MLE finite sample properties

1. Minimum Variance Unbiased Estimator (MVUE)

• Unbiased: \(E[\widehat \theta] = \theta\)

• Minimum variance: Efficiency

IF there is a MVUE, ML will find it

If not, it can still find something good enough

MLE finite sample properties

1. Minimum Variance Unbiased Estimator (MVUE)

2. Invariance to Reparameterization

• If \(\widehat \theta\) is the MLE of \(\theta\), then for any function \(f(\theta)\) its MLE is \(f(\widehat \theta)\)

• Example: \(\widehat \sigma\) is the MLE of \(\sigma\), \(\widehat \sigma^2\) is the MLE of \(\sigma^2\)

• Not true for other modes of inference!

MLE finite sample properties

1. Minimum Variance Unbiased Estimator (MVUE)

2. Invariance to Reparameterization

3. Invariance to sampling plans

• We are making not relyng on i.i.d. sampling to connect \(\theta\) and \(\widehat \theta\)

• So collecting more data after looking at results is perfectly fine!

MLE finite sample properties

1. Minimum Variance Unbiased Estimator (MVUE)

2. Invariance to Reparameterization

3. Invariance to sampling plans

In textbooks, (2) and (3) are jointly referred to as the invariance property of MLE

Asymptotic properties

1. Consistency: WLLN implies that as $ n $, the sampling distribution of the MLE collapses to a spike over the parameter value

2. Asymptotic normality: CLT implies that as \(n \rightarrow \infty\), the distribution of the standardized MLE converges to \(N(0,1)\)

3. Asymptotic efficiency: Because MLE is a sufficient statistic by definition

Lab: MLE will often give the same answers and a non-parametric estimator because the asymptotic properties are the same

What about inference?

Short answer: Normal-approximation standard errors/CIs/p-values are fine because asymptotic normality usually holds

Long answer:

You can conduct inference via likelihood-ratio tests of between parameters of interest

But too much work to test all points of interest

AM: Don’t take your models too seriously! Ok to be agnostic and compute robust/bootstrapped standard errors (more in the lab)

See here for more notes on likelihood-ratio based inference

Wrapping up

• Parametric models as alternative way to think about inference

• Makes more sense when i.i.d. is (really truly) untenable, but requires careful justification

• Estimated via MLE (alternative is method of moments)

• Many different opinions on how to deal with uncertainty

• Most people who prefer the model-based approach rely more on Bayesian statistics than MLE

• Overfitting, micronumerosity, etc. are still problems here